(本题满分12分)
如图,甲船以每小时30 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?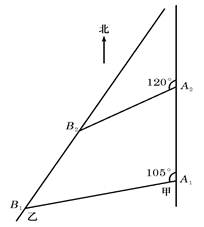
已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长。
设数列 的前
的前 项和为
项和为 ,对任意的正整数
,对任意的正整数 ,都有
,都有 成立,记
成立,记 。
。
(I)求数列 与数列
与数列 的通项公式;
的通项公式;
(II)设数列 的前
的前 项和为
项和为 ,是否存在正整数
,是否存在正整数 ,使得
,使得 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数 ;若不存在,请说明理由;
;若不存在,请说明理由;
(III)记 ,设数列
,设数列 的前
的前 项和为
项和为 ,求证:对任意正整数
,求证:对任意正整数 都有
都有 ;
;
如图,椭圆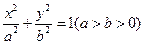 与一等轴双曲线相交,
与一等轴双曲线相交,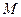 是其中一个交点,并且双曲线的顶点是该椭圆的焦点
是其中一个交点,并且双曲线的顶点是该椭圆的焦点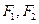 ,双曲线的焦点是椭圆的顶点
,双曲线的焦点是椭圆的顶点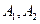 ,
,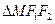 的周长为
的周长为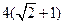 .设
.设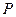 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线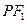 和
和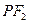 与椭圆的交点分别为
与椭圆的交点分别为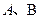 和
和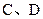 .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线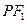 、
、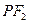 的斜率分别为
的斜率分别为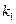 、
、 ,证明
,证明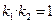 ;
;
(Ⅲ)是否存在常数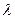 ,使得
,使得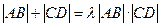 恒成立?若存在,求
恒成立?若存在,求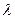 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.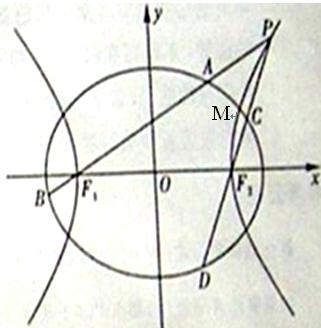
已知函数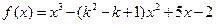 ,
, ,其中
,其中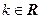 .
.
(I)设函数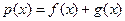 .若
.若 在区间
在区间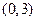 上不单调,求
上不单调,求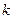 的取值范围;
的取值范围;
(II)设函数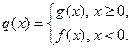 是否存在
是否存在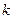 ,对任意给定的非零实数
,对任意给定的非零实数 ,存在惟一的非零实数
,存在惟一的非零实数 (
( ),使得
),使得 成立?若存在,求
成立?若存在,求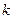 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
设数列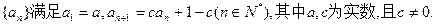
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列
(3)设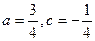 ,
,
 ,记
,记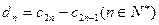 ,设数列
,设数列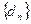 的前
的前 项和为
项和为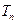 ,求证:对任意正整数
,求证:对任意正整数 都有
都有 ;
;