已知椭圆 的右焦点为
的右焦点为 ,离心率为
,离心率为 。
。
(1)若 ,求椭圆的方程。
,求椭圆的方程。
(2)设直线 与椭圆相交于
与椭圆相交于 两点,
两点, 分别为线段
分别为线段 的中点。若坐标原点
的中点。若坐标原点 在以线段
在以线段 为直径的圆上,且
为直径的圆上,且 ,求
,求 的取值范围。
的取值范围。
设函数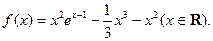
(1)求函数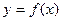 的单调区间;
的单调区间;
(2)求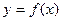 在[—1,2]上的最小值;
在[—1,2]上的最小值;
(3)当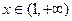 时,用数学归纳法证明:
时,用数学归纳法证明:
已知定点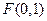 和直线
和直线 ,过定点F与直线
,过定点F与直线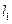 相切的动圆圆心为点C。
相切的动圆圆心为点C。
(1)求动点C的轨迹方程;
(2)过点F在直线l2交轨迹于两点P、Q,交直线l1于点R,求 的最小值。
的最小值。
济南市有大明湖、趵突泉、千佛山、园博园4个旅游景点,一位客人浏览这四个景点的概率分别是0.3,0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设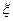 表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。
(1)求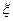 =0对应的事件的概率;
=0对应的事件的概率;
(2)求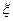 的分布列及数学期望。
的分布列及数学期望。
古代印度婆罗门教寺庙内的僧侣们曾经玩过一种被称为“河内宝塔问题”的游戏,其玩法如下:如图,设有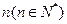 个圆盘依其半径大小,大的在下,小的在上套在
个圆盘依其半径大小,大的在下,小的在上套在 柱上,现要将套在
柱上,现要将套在 柱上的盘换到
柱上的盘换到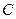 柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子
柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子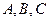 可供使用.
可供使用.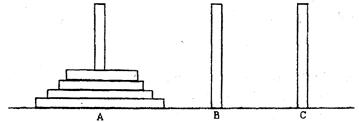
现用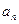 表示将
表示将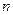 个圆盘全部从
个圆盘全部从 柱上移到
柱上移到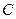 柱上所至少需要移动的次数,回答下列问题:
柱上所至少需要移动的次数,回答下列问题:
(1)写出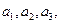 并求出
并求出
(2)记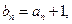 求和
求和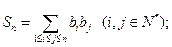 (其中
(其中 表示所有的积
表示所有的积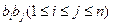 的和)
的和)
(3)证明:
已知函数
(1)求函数的单调区间;
(2)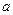 为何值时,方程
为何值时,方程 有三个不同的实根.
有三个不同的实根.