已知函数f(x)=ax3+bx2-3x在x=±1处取得极值.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤4;
(Ⅲ)若过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线,求实数m的取值范围.
已知椭圆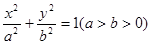 ,
,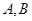 分别为左、上顶点,F为右焦点,过F作
分别为左、上顶点,F为右焦点,过F作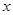 轴的垂线交椭圆于点C,且直线
轴的垂线交椭圆于点C,且直线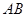 与直线OC平行.
与直线OC平行.
(1)求椭圆的离心率;
(2)已知定点M(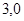 ),
),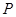 为椭圆上的动点,若
为椭圆上的动点,若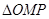 的重心轨迹经过点
的重心轨迹经过点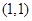 ,求椭圆的方程.
,求椭圆的方程.
已知函数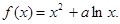
(1)当 的单调区间;
的单调区间;
(2)若函数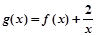 在[1,3]上是减函数,求实数a的取值范围.
在[1,3]上是减函数,求实数a的取值范围.
某日用品按行业质量标准分成五个等级,等级系数X依次为1.2.3.4.5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| X |
1 |
2 |
3 |
4 |
5 |
| f |
a |
0.2 |
0.45 |
b |
c |
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a、b、c的值;
(2)在(1)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从 这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
已知命题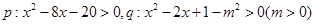 ,若
,若 是
是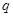 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.