已知函数 .
.
(1)画出 a =" 0" 时函数 的图象;
的图象;
(2)求函数 的最小值.
的最小值.
(本小题满分12分)
如图椭圆 的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。
的上顶点为A,左顶点为B, F为右焦点, 过F作平行与AB的直线交椭圆于C、D两点. 作平行四边形OCED, E恰在椭圆上。
(1)求椭圆的离心率;
(2)若平行四边形OCED的面积为 , 求椭圆的方程.
, 求椭圆的方程.
(本小题满分12分)
设双曲线 与直线
与直线 交于两个不同的点
交于两个不同的点 ,求双曲线
,求双曲线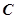 的离心率
的离心率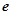 的取值范围.
的取值范围.
(本小题满分10分)
设命题 ,命题
,命题 ,若“
,若“ ”为假命题,“
”为假命题,“ ”为真命题,求实数
”为真命题,求实数 的取值范围.
的取值范围.
在平面直角坐标系中,抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO(如图所示).
(Ⅰ)求△AOB的重心G(即三角形三条中线的交点)的轨迹方程;
(Ⅱ)△AOB的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
求标准方程:
(1)若椭圆长轴长与短轴长之比为2,它的一个焦点是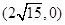 , 求椭圆的标准方程;
, 求椭圆的标准方程;
(2)若双曲线的渐近线方程为 ,它的一个焦点是
,它的一个焦点是 ,求双曲线的标准方程。
,求双曲线的标准方程。