某园林公司计划在一块
为圆心,
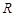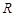(为常数，单位为米)为半径的半圆形（如图）地上种植花草树木，其中弓形
区域用于观赏样板地，
区域用于种植花木出售，其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元，花木的利润是每平方米8元，草皮的利润是每平方米3元.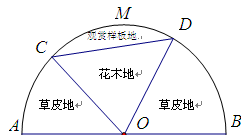
（1）设
, ,用
表示弓形的面积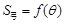
;
（2）园林公司应该怎样规划这块土地,才能使总利润最大? 并求相对应的
(参考公式:扇形面积公式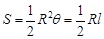
，
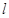表示扇形的弧长)
已知函数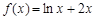
，
（1）若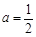
，求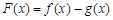
的单调区间；
（2）当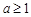
时，求证：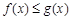
．
已知椭圆
的离心率为
，椭圆C上任意一点到椭圆两个焦点的距离之和为6。
（1）求椭圆C的方程；
（2）设直线
与椭圆C交于A、B两点，点P（0，1），且|PA|=|PB|，求直线
的方程。
已知函数
，其图象在点（1，
）处的切线方程为
（1）求a，b的值；
（2）求函数
的单调区间，并求出在区间[—2，4]上的最大值。
某校为了探索一种新的教学模式，进行了一项课题实验，乙班为实验班，甲班为对比班，甲乙两班的人数均为50人，一年后对两班进行测试，成绩如下表（总分：150分）：
甲班
| 成绩 |
 |
 |
 |
 |
 |
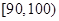| 频数 |
4 |
20 |
15 |
10 |
1 |
乙班
| 成绩 |
|
|
|
|
|
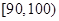| 频数 |
1 |
11 |
23 |
13 |
2 |
（1）现从甲班成绩位于
内的试卷中抽取9份进行试卷分析，请问用什么抽样方法更合理，并写出最后的抽样结果；
（2）根据所给数据可估计在这次测试中，甲班的平均分是101.8，请你估计乙班的平均分，并计算两班平均分相差几分；
（3）完成下面2×2列联表，你认为在犯错误的概率不超过0.025的前提下， “这两个班在这次测试中成绩的差异与实施课题实验有关”吗？并说明理由。
| 成绩小于100分 |
成绩不小于100分 |
合计 |
|
| 甲班 |
 |
26 |
50 |
| 乙班 |
12 |
 |
50 |
| 合计 |
36 |
64 |
100 |
附：
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
在平面直角坐标系xOy中，抛物线C的顶点在原点，经过点A(2,2)，其焦点F在x轴上．
(1)求抛物线C的标准方程；
(2)设直线l是抛物线的准线，求证：以AB为直径的圆与准线l相切．