一袋中有6个黑球,4个白球.
(1)依次取出3个球,不放回,已知第一次取出的是白球,求第三次取到黑球的概率;
(2)有放回地依次取出3球,已知第一次取的是白球,求第三次取到黑球的概率;
(3)有放回地依次取出3球,求取到白球个数X的分布列、期望和方差.
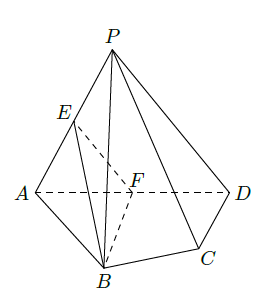
如图,在四棱锥
中,平面
平面
,
,
,
分别是
的中点.
求证:(1)直线
平面
;
(2)平面
平面
.
在 中,角 所对应的边为
(1)若
,求
的值;
(2)若
,求
的值.
在平面直角坐标系 上,给定抛物线 .实数 满足 , 是方程 的两根,记
(1)过点 作 的切线教 轴于点 .证明:对线段 上任一点 有 ;
(2)设 是定点,其中 满足 , .过 作 的两条切线 ,切点分别为 , 与y轴分别交与 .线段 上异于两端点的点集记为 .证明: ;
(3)设 .当点 取遍 时,求 的最小值(记为 )和最大值(记为 ).
设 ,数列 满足 , ,
(1)求数列 的通项公式.
(2)证明:对于一切正整数 ,
设圆 与两圆 中的一个内切,另一个外切.
(1)求 的圆心轨迹 的方程.
(2)已知点 , 且 为 上动点,求 的最大值及此时点 的坐标.