为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度x（单位：cm）满足关系：C（x）=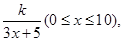
若不建隔热层（即x=0时），每年能源消耗费用为8万元.设f（x）为隔热层建造费用与20年的能源消耗费用之和.
（1）求k的值；
（2）求f(x)的表达式；
（3）利用“函数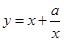
（其中
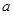为大于0的常数），在
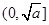上是减函数，在
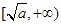上是增函数”这一性质，求隔热层修建多厚时，总费用f(x)达到最小，并求出这个最小值.
（本小题满分10分）已知向量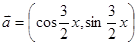
，
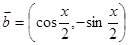，且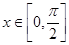
，
（1）求a·b及|a＋b|；
（2）若f（x）＝a·b－2λ|a＋b|的最小值是－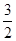
，求λ的值．
（本小题满分8分）已知函数
（1）求f（x）的定义域及最小正周期
（2）求f（x）的单调递减区间．
（本小题满分8分）如图给出了一个程序框图，其功能是输入x的值，输出相应的y的值．
（1）写出相应的程序；
（2）如果输入的x的值与输出的y的值相等，试求出满足条件的所有x的值．
（本小题满分8分）已知△ABC顶点的直角坐标分别为A（3，4），B（0，0），C（c，0）．
（1）若c＝5，求sin∠A的值；
（2）若∠A是钝角，求c的取值范围
（本小题满分6分）已知函数
，
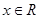
（1）求y取最大值时相应的x的集合；
（2）该函数的图象经过怎样的平移和伸缩变换可以得到函数y＝sin x（x∈R）的图象．