已知函数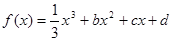 ,设曲线
,设曲线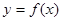 在与
在与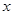 轴交点处的切线为
轴交点处的切线为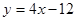 ,
,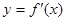 为
为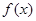 的导函数,满足
的导函数,满足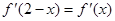 .
.
(1)求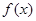 ;
;
(2)设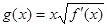 ,
,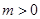 ,求函数
,求函数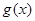 在
在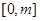 上的最大值;
上的最大值;
(3)设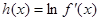 ,若对于一切
,若对于一切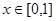 ,不等式
,不等式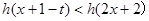 恒成立,求实数
恒成立,求实数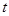 的取值范围.
的取值范围.
设 是定义在R上的偶函数,其图象关于直线
是定义在R上的偶函数,其图象关于直线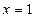 对称,证明
对称,证明 是周期函数.
是周期函数.
在直角坐标平面中, 的两个顶点分别
的两个顶点分别 的坐标为
的坐标为 ,
, ,平面内两点
,平面内两点 同时满足下列条件:
同时满足下列条件:
① ;②
;② ;③
;③ ∥
∥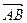
(1)求 的顶点
的顶点 的轨迹方程;
的轨迹方程;
(2)过点 的直线
的直线 与(1)中轨迹交于
与(1)中轨迹交于 两点,求
两点,求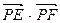 的取值范围
的取值范围
如图所示,B(– c,0),C(c,0),AH⊥BC,垂足为H,且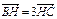 .
.
(1)若 = 0,求以B、C为焦点并且经过点A的椭圆的离心率;
= 0,求以B、C为焦点并且经过点A的椭圆的离心率;
(2)D分有向线段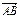 的比为
的比为 ,A、D同在以B、C为焦点的椭圆上,当 ―5≤
,A、D同在以B、C为焦点的椭圆上,当 ―5≤ ≤
≤ 时,求椭圆的离心率e的取值范围.
时,求椭圆的离心率e的取值范围.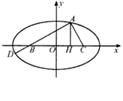
设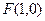 ,
,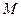 、
、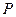 分别为
分别为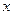 轴、
轴、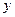 轴上的点,且
轴上的点,且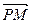

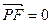 ,动点
,动点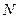 满足:
满足: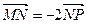 .
.
(1)求动点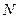 的轨迹
的轨迹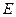 的方程;
的方程;
(2)过定点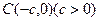 任意作一条直线
任意作一条直线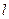 与曲线
与曲线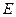 交与不同的两点
交与不同的两点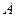 、
、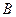 ,问在
,问在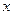 轴上是否存在一定点
轴上是否存在一定点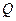 ,使得直线
,使得直线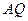 、
、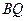 的倾斜角互补?若存在,求出
的倾斜角互补?若存在,求出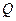 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
设椭圆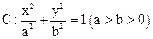 过点
过点 ,且焦点为
,且焦点为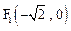 。
。
(1)求椭圆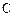 的方程;
的方程;
(2)当过点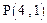 的动直线
的动直线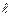 与椭圆
与椭圆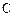 相交与两不同点A、B时,在线段
相交与两不同点A、B时,在线段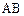 上取点
上取点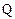 ,
,
满足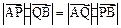 ,证明:点
,证明:点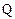 总在某定直线上。
总在某定直线上。