已知函数 满足:对于任意实数
满足:对于任意实数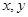 ,都有
,都有 恒成立,且当
恒成立,且当 时,
时,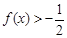 恒成立;
恒成立;
(1)求 的值,并例举满足题设条件的一个特殊的具体函数;
的值,并例举满足题设条件的一个特殊的具体函数;
(2)判定函数 在R上的单调性,并加以证明;
在R上的单调性,并加以证明;
(3)若函数 (其中
(其中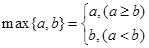 )有三个零点
)有三个零点 ,求
,求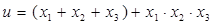 的取值范围.
的取值范围.
(本小题11分)如图,三棱锥C—ABD,CB = CD,AB = AD,∠BAD = 90°。E、F分别是BC、AC的中点。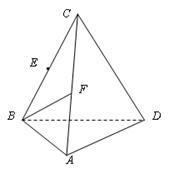
(1)求证:AC⊥BD;
(2)若CA = CB,求证:平面BCD⊥平面ABD
(3)在 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出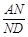 的值
的值
(本小题11分)如图,在四棱锥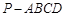 中,
中,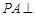 平面
平面 ,
,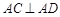 ,
,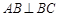 ,
, ,
,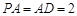 ,
, .
.
(1)证明: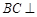 平面
平面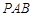
(2)求 和平面
和平面 所成角的正弦值
所成角的正弦值
(3)求二面角 的正切值;
的正切值;
(本小题8分)如图所示,在正三棱柱 中,若
中,若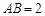 ,
,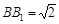 ,
,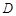 是
是 中点。
中点。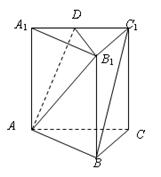
(1)证明: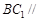 平面
平面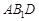 ;
;
(2)求 与
与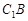 所成的角的大小。
所成的角的大小。
(本小题9分)如图是一个空间几何体的三视图,其正视图与侧视图是边长为4cm的正三角形、俯视图中正方形的边长为4cm,
(1)画出这个几何体的直观图(不用写作图步骤);
(2)请写出这个几何体的名称,并指出它的高是多少;
(3)求出这个几何体的表面积。
已知抛物线 过点
过点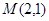 .
.
(I)求抛物线的方程;
(II)已知圆心在 轴上的圆
轴上的圆 过点
过点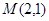 ,且圆
,且圆 在点
在点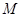 的切线恰是抛物线在点
的切线恰是抛物线在点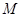 的切线,求圆
的切线,求圆 的方程;
的方程;
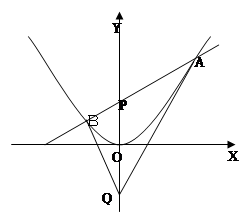
(Ⅲ)如图,点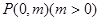 为
为 轴上一点,点
轴上一点,点 是点
是点 关于原点的对称点,过点
关于原点的对称点,过点 作一条直线与抛物线交于
作一条直线与抛物线交于 两点,若
两点,若 ,证明:
,证明: .
.