某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的体积为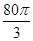
立方米，且
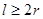．假设该容器的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为
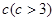千元，设该容器的建造费用为
千元．
（1）写出关于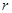
的函数表达式，并求该函数的定义域；
（2）求该容器的建造费用最小时的．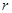
已知函数
.
（1）用“五点法”画出函数f（x）在［0，
］上的简图；
（2）在△ABC中，a，b，c分别是角A，B，C的对边，f（A）=1，
，b+c=3（b＞c），求b，c的长.
已知0＜a＜1，判断函数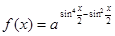
的奇偶性，并求出函数f（x）的周期.
设α∈（0，
），f（x）的定义域为［0，1］，f（0）=0，f（1）=1，当x≥y时，有
，求
、
.
已知函数
.
（1）当a=1时，求函数f（x）的单调递增区间；
（2）（ⅰ）当a＜0且x∈［0，π］时，函数f（x）的值域是［3，4］，求a+b的值；
（ⅱ）当a＜0时，函数f（x）的值域是［3，4］，求a+b的值.
已知向量a=（cosx，sinx），b=（sin2x，1-cos2x），c=（0，1），x∈（0，π）.
（1）向量a、b是否共线?请证明你的结论.
（2）若函数f（x）=|b|-（a+b）·c，求f（x）的最小值，并指出取得最小值时的x值.