为了调查胃病是否与生活规律有关,调查某地540名40岁以上的人得结果如下:
| |
患胃病 |
未患胃病 |
合计 |
| 生活不规律 |
60 |
260 |
320 |
| 生活有规律 |
20 |
200 |
220 |
| 合计 |
80 |
460 |
540 |
根据以上数据回答40岁以上的人患胃病与生活规律有关吗?
本题满分14分)
为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查,测得身高频数分布表如下表1、表2.
表1:男 生身高频数分布表
生身高频数分布表
表2:女生身高频数分布表
(1)求该校男生的人数并完成下面频率分布直方图;
(2)估计该校学生身高(单位:cm)在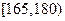 的概率;
的概率;
(3)在男生样本中,从身高(单位:cm)在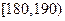 的男生中任选3人,设
的男生中任选3人,设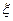 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在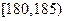 的人数,求
的人数,求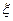 的分布列和数学期望.
的分布列和数学期望.
已知函数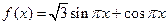 ,
,  .
.
(1)求函数 的最大值和最小值;
的最大值和最小值;
(2)设函数 在
在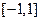 上的图象与
上的图象与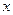 轴的交点从左到右分别为M、N,图象的最高点为P,求
轴的交点从左到右分别为M、N,图象的最高点为P,求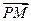 与
与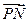 的夹角的余弦
的夹角的余弦
(本小题共14分)
如图,四棱锥 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.
(Ⅰ)求证:平面 ;
;
(Ⅱ)当 且E为PB的中点时,求AE与平面PDB所成的角的大小.
且E为PB的中点时,求AE与平面PDB所成的角的大小.
(本小题共13分)直线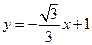 和
和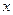 轴,
轴,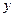 轴分别交于点
轴分别交于点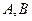 ,以线段
,以线段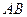 为边在第一象限内作等边△
为边在第一象限内作等边△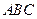 ,如果在第一象限内有一点
,如果在第一象限内有一点 使得△
使得△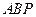 和△
和△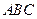 的面积相等, 求
的面积相等, 求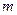 的值。
的值。
(本小题共12分)北京奥运会纪念章某特许专营店销售纪念章,每枚进价为5元,同时每销售一枚这种纪念章还需向北京奥组委交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为x元(x∈N*).(Ⅰ)写出该特许专营店一年内销售这种纪念章所获得的利润y(元)与每枚纪念章的销售价格x的函数关系式(并写出这个函数的定义域);(Ⅱ)当每枚纪念销售价格x为多少元时,该特许专营店一年内利润y(元)最大,并求出这个最大值.