为了研究某种细菌随时间x变化的繁殖个数，收集数据如下：
天数 |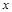
1 |
2 |
3 |
4 |
5 |
6 |
繁殖个数 |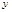
6 |
12 |
25 |
49 |
95 |
190 |
（1）作出这些数据的散点图；
（2）求出y对x的回归方程．
（本题满分14分，第1小题4分，第2小题5分，第3小题5分）平面直角坐标系中，
为原点，射线
与
轴正半轴重合，射线
是第一象限角平分线．在上有点列
，
，在上有点列
，
，．已知
，
，
．
（1）求点
的坐标；
（2）求
的坐标；
（3）求
面积的最大值，并说明理由．
（本题满分10分，第1小题5分，第2小题5分）等比数列{an}的前n项的和为Sn，已知S1，S3，S2成等差数列.
（1）求{an}的公比q；
（2）若a1-a3=3,求
.
（本题满分
分，第1小题4分，第2小题4分）已知直角坐标平面中，
为坐标原点，
．
（1）求
的大小（结果用反三角函数值表示）；
（2）设点
为
轴上一点，求
的最大值及取得最大值时点的坐标．
（本题满分
分）用行列式解关于
的方程组：
，并对解的情况进行讨论．
（本题满分
分，第1小题4分，第2小题4分）已知
，
,且向量
与
不共线.
（1）若与的夹角为
，求
·
；
（2）若向量
与
互相垂直，求
的值.