双曲线＝1(a<0，b<0)的离心率为2，坐标原点到直线AB-优题课

双曲线＝1(a>0，b>0)的离心率为2，坐标原点到直线AB的距离为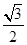，其中A(0，－b)，B(a,0)．
(1)求双曲线的标准方程；
(2)设F是双曲线的右焦点，直线l过点F且与双曲线的右支交于不同的两点P、Q，点M为线段PQ的中点．若点M在直线x＝－2上的射影为N，满足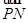·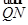＝0，且|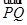|＝10，求直线l的方程．

科目数学题型解答题难度容易

设α∈R，f（x）=cosx（asinx﹣cosx）+cos²（﹣x）满足，求函数f（x）在上的最大值和最小值．

设实数数列{a_n}的前n项和S_n满足S_n+1=a_n+1S_n（n∈N^*）．
（1）若a₁，S₂，﹣2a₂成等比数列，求S₂和a₃．
（2）求证：对k≥3有0≤a_k≤．

设函数 $f (x) = (x - a) 2 \ln x, a \in R$

（1）若 $x = e$ 为 $y = f (x)$ 的极值点，求实数 $a$ ；
（2）求实数 $a$ 的取值范围，使得对任意的 $x \in (0, 3 e]$ ，恒有 $f (x) \leq 4 e 2$ 成立．注：e为自然对数的底数．

已知抛物线 $C_{1}$ ： $x^{2} = y$ ，圆 $C_{2}$ ： $x^{2} + {(y - 4)}^{2} = 1$ 圆心为点 $M$

（1）求点 $M$ 到抛物线 $C_{1}$ 的准线的距离；
（2）已知点 $P$ 是抛物线 $C_{1}$ 上一点（异于原点），过点 $P$ 作圆 $C_{2}$ 的两条切线，交抛物线 $C_{1}$ 于 $A, B$ 两点，若过 $M, P$ 两点的直线 $l$ 垂直于 $A B$ ，求直线 $l$ 的方程．

如图,在三棱锥 $P - A B C$ 中, $A B = A C, D$ 为 $B C$ 的中点, $P O ⊥$ 平面 $A B C$ ,垂足 $O$ 落在线段 $A D$ 上,已知 $B C = 8, P O = 4, A O = 3, O D = 2$

（1）证明: $A P ⊥ B C$ ；

（2）在线段 $A P$ 上是否存在点 $M$ ,使得二面角 $A - M C - β$ 为直二面角？若存在,求出 $A M$ 的长;若不存在,请说明理由．

试卷网试题网古诗词网作文网范文网