[选修4 - 1:几何证明选讲](本小题满分10分)
如图,在梯形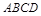 中,
中,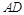 ∥BC,点
∥BC,点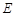 ,
,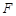 分别在边
分别在边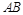 ,
,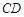 上,设
上,设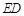 与
与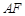 相交于点
相交于点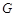 ,若
,若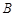 ,
,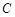 ,
,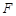 ,
,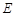 四点共圆,求证:
四点共圆,求证: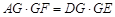 .
. 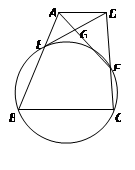
正实数数列
中,
,且
成等差数列.
(1) 证明数列
中有无穷多项为无理数;
(2)当
为何值时,
为整数,并求出使
的所有整数项的和.
已知抛物线
经过椭圆
的两个焦点. 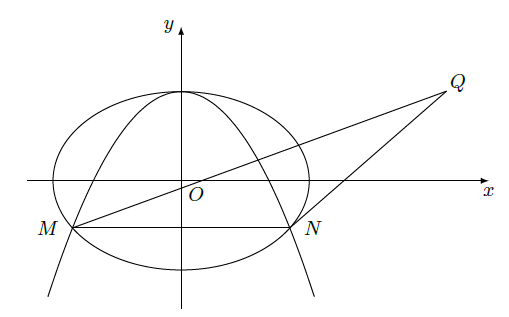
(1) 求椭圆
的离心率;
(2) 设
,又
为
与
不在
轴上的两个交点,若
的重心在抛物线
上,求
和
的方程.
如图, 与 都是边长为2的正三角形,平面 平面 , 平面 ,

(1)求直线
与平面
所成的角的大小;
(2)求平面
与平面
所成的二面角的正弦值.
已知函数
.
(1)若
,求
;
(2)若
,求
的取值范围.
某迷宫有三个通道,进入迷宫的每个人都要经过一扇智能门。首次到达此门,系统会随机(即等可能)为你打开一个通道.若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门.再次到达智能门时,系统会随机打开一个你未到过的通道,直至走出迷宫为止.
(1)求走出迷宫时恰好用了1小时的概率;
(2)求走出迷宫的时间超过3小时的概率.