如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,
OC=OE=4,DB⊥DC,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交
于M.点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.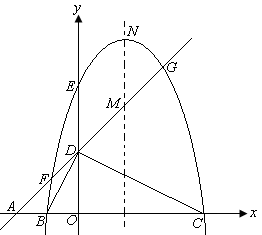
(1)求经过B、E、C三点的抛物线的解析式;
(2)是否存在点P,使得以P、Q、M为顶点的三角形与△AOD相似?若存在,求出满足条件
的点P的坐标;若不存在,请说明理由;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成
为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
已知 为实数,
为实数,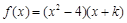 .
.
(1)求导数 ;
;
(2)若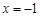 是函数
是函数 的极值点,求
的极值点,求 在区间
在区间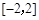 上的最大值和最小值;
上的最大值和最小值;
(3)若 在区间
在区间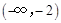 和
和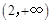 上都是单调递增的,求实数
上都是单调递增的,求实数 的取值范围.
的取值范围.
对于企业来说,生产成本、销售收入和利润之间的关系是个重要的问题.对一家药品生产企业的研究表明:该企业的生产成本 (单位:万元)和生产收入
(单位:万元)和生产收入 (单位:万元)都是产量
(单位:万元)都是产量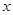 (单位:
(单位: )的函数,它们分别为
)的函数,它们分别为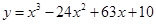 和
和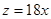 .
.
(1)试求出该企业获得的生产利润 (单位:万元)与产量
(单位:万元)与产量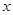 之间的函数关系式;
之间的函数关系式;
(2)当产量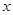 为多少时,该企业可获得最大利润?最大利润为多少?
为多少时,该企业可获得最大利润?最大利润为多少?
已知函数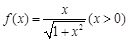 ,数列
,数列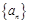 满足
满足 ,
, .
.
(1)求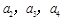 ;
;
(2)猜想数列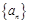 的通项,并用数学归纳法予以证明.
的通项,并用数学归纳法予以证明.
(1)若 的展开式中,
的展开式中,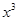 的系数是
的系数是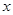 的系数的
的系数的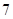 倍,求
倍,求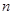 ;
;
(2)已知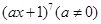 的展开式中,
的展开式中, 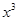 的系数是
的系数是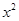 的系数与
的系数与 的系数的等差中项,求
的系数的等差中项,求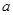 ;
;
(3)已知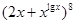 的展开式中,二项式系数最大的项的值等于
的展开式中,二项式系数最大的项的值等于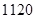 ,求
,求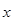 .
.
已知复数 ,当实数
,当实数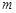 为何值时:
为何值时:
(1)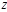 为实数;
为实数;
(2) 为虚数;
为虚数;
(3) 为纯虚数;
为纯虚数;
(4)复数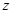 对应的点
对应的点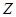 在第四象限.
在第四象限.