某市在城市建设中要拆除旧烟囱AB（如图所示），在烟囱正西方向的楼CD的顶端C处测得烟囱的顶端A的仰角为45°，底端B的俯角为30°，已量得DB=21
.
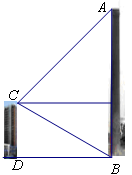
（1）在原图上画出点C望点A的仰角和点C望点B的俯角，并分别标出仰角和俯角的大小；
（2）拆除时若让烟囱向正东倒下，试问：距离烟囱东方35远的一棵大树是否被歪倒的烟囱砸着？请说明理由.
解方程：6x+2=4x-5
如图，直线AB、CD、EF相交于点O，AB⊥CD，OG平分∠AOE，∠FOD=280，求∠AOG的度数.
列方程解应用题：某商场以每台1980元的价格购进一批彩电，进货时按当时的市场行情，制定的销售价为每台2640元.销售一段时间后，由于市场竞争激烈，商场决定降价销售.如果销售每台仍能获利20%，那么应该按原销售价的几折出售？
列方程解应用题：七年级某班同学清明节去扫墓，步行的同学先从学校出发1h，然后骑车的同学从学校出发沿同一路线前行，30min后与步行的同学同时到达.已知骑车的同学比步行的同学每小时多行10km，求骑车的同学和步行的同学的速度.
小明每天从家去学校上学行走的路程为900米，某天他从家去上学时以每分30米的速度行走了450米，为了不迟到，他加快了速度，以每分45米的速度行走完剩下的路程，那么小明行走过的路程S(米)与他行走的时间t(分)之间的函数关系用图象表示正确的是