如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8㎝,BC=4㎝,AB=5㎝.从初始时刻开始,动点P沿着P、Q分别从点A,B同时出发,运动速度均为1㎝/s,动点P沿A—B—C—E的方向运动,到点E停止;动点Q沿B—C—E—D的方向运动,到点D停止,设运动时间为 s,△PAQ的面积为
s,△PAQ的面积为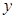 ㎝2.(这里我们把线段的面积看作是0)
㎝2.(这里我们把线段的面积看作是0)
解答下列问题
(1)当 =2s时,
=2s时,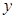 = ㎝2,当
= ㎝2,当 s时,
s时,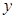 = ㎝2;
= ㎝2;
(2)当5≤ ≤14时,求
≤14时,求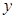 与
与 之间的函数关系式;
之间的函数关系式;
(3)当动点P在线段BC上运动时,求出
 梯形ABCD时
梯形ABCD时 的值;
的值;
(4)直接写出整个运动过程中,使PQ与四边形ABCE的对角线平行的所有 的值.
的值.
我们知道,经过原点的抛物线可以用 表示,对于这样的抛物线:
(1)当抛物线经过点 和 时,求抛物线的表达式;
(2)当抛物线的顶点在直线 上时,求 的值;
(3)如图,现有一组这样的抛物线,它们的顶点 、 、 , 在直线 上,横坐标依次为 , , , , 为正整数,且 ,分别过每个顶点作 轴的垂线,垂足记为 、 , , ,以线段 为边向左作正方形 ,如果这组抛物线中的某一条经过点 ,求此时满足条件的正方形 的边长.

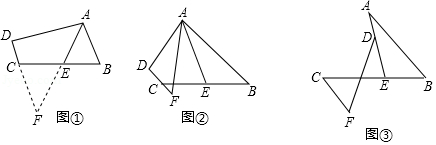
(1)阅读理解:如图①,在四边形 中, , 是 的中点,若 是 的平分线,试判断 , , 之间的等量关系.
解决此问题可以用如下方法:延长 交 的延长线于点 ,易证 ,得到 ,从而把 , , 转化在一个三角形中即可判断.
、 、 之间的等量关系为 ;
(2)问题探究:如图②,在四边形 中, , 与 的延长线交于点 , 是 的中点,若 是 的平分线,试探究 , , 之间的等量关系,并证明你的结论.
(3)问题解决:如图③, , 与 交于点 , ,点 在线段 上,且 ,试判断 、 、 之间的数量关系,并证明你的结论.
如图,直线 与反比例函数 的图象交于点 ,与 轴交于点 ,平行于 轴的直线 交反比例函数的图象于点 ,交 于点 ,连接 .
(1)求 的值和反比例函数的表达式;
(2)直线 沿 轴方向平移,当 为何值时, 的面积最大?

如图, 、 是半圆 上的三等分点,直径 ,连接 、 , ,垂足为 , 交 于点 .
(1)求 的度数;
(2)求阴影部分的面积(结果保留 和根号).

“2017年张学友演唱会”于6月3日在我市观山湖奥体中心举办,小张去离家2520米的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有23分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小张骑车的时间比跑步的时间少用了4分钟,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度;
(2)如果小张在家取票和寻找“共享单车”共用了5分钟,他能否在演唱会开始前赶到奥体中心?说明理由.