(本小题满分12分)甲、乙两袋中各装有大小相同的小球9个,其中甲袋中红色、黑色、白色小球的个数分别为2,3,4,乙袋中红色、黑色、白色小球的个数均为3,某人用左右手分别从甲、乙两袋中取球.
(Ⅰ)若左右手各取一球,求两只手中所取的球颜色不同的概率;
(Ⅱ)若左右手依次各取两球,称同一手中 两球颜色相同的取法为成功取法,记两次取球(左右手依次各取两球为两次取球)的成功取法次数为随机变量X,求X的分布列和数学期望.
(本小题满分10分)已知集合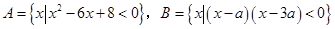 .
.
(Ⅰ)若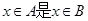 的充分条件,求
的充分条件,求 的取值范围;
的取值范围;
(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.
已知函数
⑴解不等式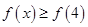 ;
;
⑵设函数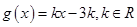 ,若不等式
,若不等式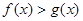 恒成立,求实数
恒成立,求实数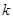 的取值范围.
的取值范围.
已知曲线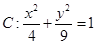 ,直线
,直线 (t为参数).
(t为参数).
(1)写出曲线C的参数方程,直线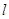 的普通方程;
的普通方程;
(2)过曲线C上任意一点P作与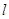 夹角为30°的直线,交
夹角为30°的直线,交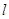 于点A,求|PA|的最大值与最小值.
于点A,求|PA|的最大值与最小值.
如图,圆周角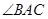 的平分线与圆交于点
的平分线与圆交于点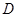 ,过点
,过点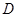 的切线与弦
的切线与弦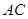 的延长线交于点
的延长线交于点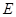 ,
, 交
交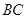 于点
于点 .
.
(1)求证: ;
;
(2)若 四点共圆,且弧
四点共圆,且弧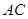 与弧
与弧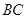 相等,求
相等,求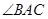 .
.