如图, 是棱长为
是棱长为 的正方体,
的正方体, 、
、 分别是棱
分别是棱 、
、 上的动点,且
上的动点,且 .
.
(1)求证: ;
;
(2)当 、
、 、
、 、
、 共面时,求:面
共面时,求:面 与面
与面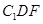 所成二面角的余弦值.
所成二面角的余弦值.
.(本小题满分14分)
如图,在边长为10的正三角形纸片ABC的边AB,AC上分别取D,E两点,使沿线段DE折叠三角形纸片后,顶点A正好落在边BC上(设为P),在这种情况下,求AD的最小值.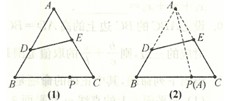
(本小题满分14分)
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=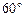 ,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.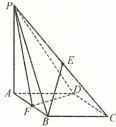
(1)求证:BE∥平面PDF;
(2)求证:平面PDF⊥平面PAB;
(3)求三棱锥P-DEF的体积.
(本小题满分14分)
已知点A(3,0),B(0,3),C(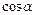 ,
,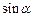 ),
),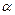 ∈
∈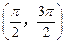 .
.
(1)若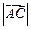 =
=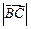 ,求角
,求角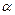 的值;
的值;
(2)若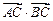 =-1,求
=-1,求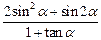 的值.
的值.
(本小题满分16分)
已知函数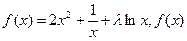 的导数是
的导数是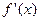 .
.
(1)求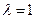 时,
时,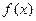 在x=1处的切线方程。
在x=1处的切线方程。
(2)当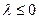 时,求证:对于任意的两个不等的正数
时,求证:对于任意的两个不等的正数 ,有
,有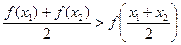 ;
;
(3)对于任意的两个不等的正数 ,若
,若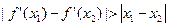 恒成立,求
恒成立,求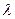 的取值范围.
的取值范围.
(本小题满分16分)
已知数列﹛an﹜中,a2=p(p是不等于0的常数),Sn为数列﹛an﹜的前n项和,若对任意的正整数n都有Sn= .
.
(1)证明:数列﹛an﹜为等差数列;
(2)记bn= +
+ ,求数列﹛bn﹜的前n项和Tn;
,求数列﹛bn﹜的前n项和Tn;
(3)记cn=Tn-2n,是否存在正整数m,使得当n>m时,恒有cn∈(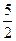 ,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。
,3)?若存在,证明你的结论,并给出一个具体的m值;若不存在,请说明理由。