甲有一个箱子,里面放有x个红球,y个白球(x,y≥0,且x+y=4);乙有一个箱子,里面放有2个红球,1个白球,1个黄球.现在甲从箱子里任取2个球,乙从箱子里任取1个球.若取出的3个球颜色全不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色球的个数,才能使自己获胜的概率最大?
(2)在(1)的条件下,求取出的3个球中红球个数的期望.
在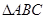 中,角
中,角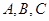 对的边分别为
对的边分别为 ,已知
,已知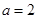 .
.
(1)若 ,求
,求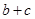 的取值范围;
的取值范围;
(2)若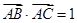 ,求
,求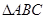 面积的最大值.
面积的最大值.
已知函数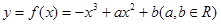
(1)若函数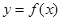 的图象切x轴于点(2,0),求a、b的值;
的图象切x轴于点(2,0),求a、b的值;
(2)设函数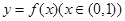 的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求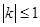 的充要条件;
的充要条件;
(3)若函数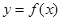 的图象上任意不同的两点的连线的斜率小于l,求证
的图象上任意不同的两点的连线的斜率小于l,求证 .
.
给定椭圆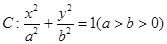 .称圆心在原点O,半径为
.称圆心在原点O,半径为 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为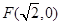 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为 .
.
(1)求椭圆C的方程和其“准圆”方程;
(2)点P是椭圆C的“准圆”上的一个动点,过动点P作直线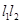 ,使得
,使得 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断 是否垂直?并说明理由.
是否垂直?并说明理由.
如图,长方体 中,
中,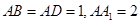 ,G是
,G是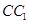 上的动点。
上的动点。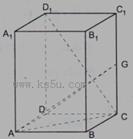
(l)求证:平面ADG
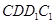 ;
;
(2)判断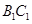 与平面ADG的位置关系,并给出证明;
与平面ADG的位置关系,并给出证明;
(3)若G是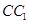 的中点,求二面角G-AD-C的大小;
的中点,求二面角G-AD-C的大小;
甲、乙两人各掷一次骰子(均匀的正方体,六个面上分别为1,2,3,4,5,6点),所得点数分别为x,y
(1)求x<y的概率;
(2)求5<x+y<10的概率。