某工厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品,根据以往的经验知道,其次品率P与日产量 (件)之间近似满足关系:
(件)之间近似满足关系: (其中
(其中 为小于96的正整常数)
为小于96的正整常数)
(注:次品率P= ,如P=0.1表示每生产10件产品,有1件次品,其余为合格品.)已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损A/2元,故厂方希望定出合适的日产量。
,如P=0.1表示每生产10件产品,有1件次品,其余为合格品.)已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损A/2元,故厂方希望定出合适的日产量。
试将生产这种仪器每天的赢利T(元)表示为日产量 (件的函数);
(件的函数);
当日产量为多少时,可获得最大利润?
切线 与圆切于点
与圆切于点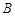 ,圆内有一点
,圆内有一点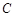 满足
满足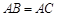 ,
,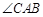 的平分线
的平分线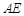 交圆于
交圆于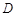 ,
,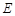 ,延长
,延长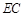 交圆于
交圆于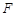 ,延长
,延长 交圆于
交圆于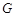 ,连接
,连接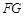 .
.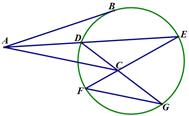
(Ⅰ)证明: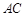 //
//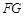 ;
;
(Ⅱ)求证: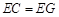 .
.
已知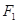 ,
,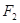 分别是椭圆
分别是椭圆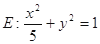 的左、右焦点
的左、右焦点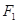 ,
,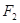 关于直线
关于直线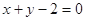 的对称点是圆
的对称点是圆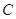 的一条直径的两个端点.
的一条直径的两个端点.
(Ⅰ)求圆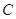 的方程;
的方程;
(Ⅱ)设过点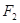 的直线
的直线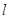 被椭圆
被椭圆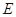 和圆
和圆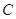 所截得的弦长分别为
所截得的弦长分别为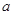 ,
,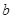 .当
.当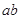 最大时,求直线
最大时,求直线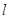 的方程.
的方程.
已知函数 .
.
(Ⅰ)讨论函数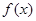 的单调区间;
的单调区间;
(Ⅱ)当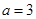 时,若函数
时,若函数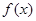 在区间
在区间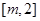 上的最大值为28,求
上的最大值为28,求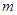 的取值范围.
的取值范围.
将棱长为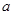 的正方体截去一半(如图甲所示)得到如图乙所示的几何体,点
的正方体截去一半(如图甲所示)得到如图乙所示的几何体,点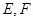 分别是
分别是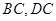 的中点.
的中点.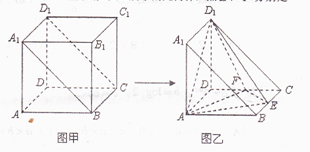
(Ⅰ)证明: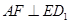 ;
;
(Ⅱ)求三棱锥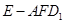 的体积.
的体积.
为了加强中学生实践、创新能力和团队精神的培养,促进教育教学改革,市教育局举办了全市中学生创新知识竞赛,某中学举行了选拔赛,共有150名学生参加,为了了解成绩情况,从中抽取了50名学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成的频率分布表,解答下列问题:
(Ⅰ)完成频率分布表(直接写出结果),并作出频率分布直方图;
(Ⅱ)若成绩在95.5分以上的学生为一等奖,试估计全校获一等奖的人数,现在从全校所有一等奖的同学中随机抽取2名同学代表学校参加决赛,某班共有2名同学荣获一等奖,求该班同学参加决赛的人数恰为1人的概率.