在数列{an}中,a1=1,当n≥2时,其前n项和Sn满足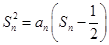 .
.
(1)求Sn的表达式;
(2)设bn=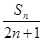 ,求{bn}的前n项和Tn.
,求{bn}的前n项和Tn.
(本小题满分7分)《选修4-4:坐标系与参数方程》
在极坐标系中,圆 的极坐标方程为
的极坐标方程为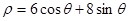 .现以极点
.现以极点 为原点,极轴为
为原点,极轴为 轴的非负半轴建立平面直角坐标系.
轴的非负半轴建立平面直角坐标系.
(Ⅰ)求圆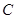 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若圆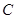 上的动点
上的动点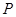 的直角坐标为
的直角坐标为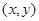 ,求
,求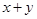 的最大值,并写出
的最大值,并写出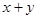 取得最大值时点P的直角坐标.
取得最大值时点P的直角坐标.
(本小题满分7分)选修4—2:矩阵与变换
如图,单位正方形区域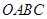 在二阶矩阵
在二阶矩阵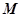 的作用下变成平行四边形
的作用下变成平行四边形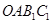 区域.
区域.
(Ⅰ)求矩阵 ;
;
(Ⅱ)求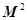 ,并判断
,并判断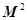 是否存在逆矩阵?若存在,求出它的逆矩阵.
是否存在逆矩阵?若存在,求出它的逆矩阵.
已知函数 ,其中
,其中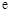 是自然对数的底数.
是自然对数的底数.
(Ⅰ)求函数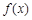 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若函数 对任意
对任意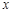 满足
满足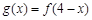 ,求证:当
,求证:当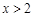 时,
时,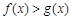 ;
;
(Ⅲ)若 ,且
,且 ,求证:
,求证:
设椭圆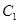 :
: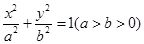 的左、右焦点分别是
的左、右焦点分别是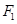 、
、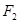 ,下顶点为
,下顶点为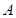 ,线段
,线段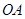 的中点为
的中点为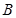 (
(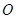 为坐标原点),如图.若抛物线
为坐标原点),如图.若抛物线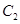 :
: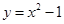 与
与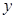 轴的交点为
轴的交点为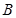 ,且经过
,且经过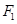 、
、 两点.
两点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设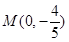 ,
,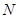 为抛物线
为抛物线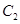 上的一动点,过点
上的一动点,过点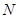 作抛物线
作抛物线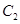 的切线交椭圆
的切线交椭圆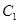 于
于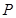 、
、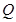 两点,求
两点,求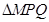 面积的最大值.
面积的最大值.
如图所示,机器人海宝按照以下程序运行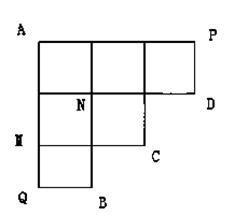
①从A出发到达点B或C或D,到达点B、C、D之一就停止;
②每次只向右或向下按路线运行;
③在每个路口向下的概率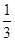 ;
;
④到达P时只向下,到达Q点只向右.
(1)求海宝过点从A经过M到点B的概率,求海宝过点从A经过N到点C的概率;
(2)记海宝到点B、C、D的事件分别记为X=1,X=2,X=3,求随机变量X的分布列及期望.