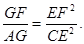已知函数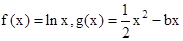
（b为常数）.
（1）函数f(x)的图像在点（1，f(1)）处的切线与g(x)的图像相切，求实数b的值；
（2）设h(x)=f(x)+g(x),若函数h(x)在定义域上存在单调减区间，求实数b 的取值范围；
（3）若b>1,对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)-f(x2)|> |g(x1)-g(x2)|成立，求b的取值范围.
在△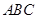
中，角
、
、
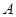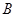的对边分别为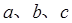
，满足
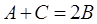，且.
（1）求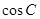
的值； （2）若
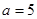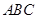，求△的面积.
在直角坐标系
中，点p到两点
的距离之和等于4，
设点P的轨迹为C，直线
与C交于A、B两点，
（1）写出C的方程；
（2）若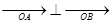
，求k的值。
设函数
．
（1）求不等式
的解集；
（2）若不等式
的解集是非空的集合，求实数
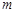的取值范围．
以平面直角坐标系的坐标原点为极点，
轴的非负半轴为极轴建立极坐标系，曲线E的极坐标方程为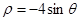
，曲线F的参数方程为
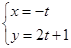（t为参数）
(1) 求曲线E的直角坐标方程及曲线F的普通方程；
(2)判断两直线的位置关系，若相交，求弦长，若不相交，说明理由。
如图，已知⊙O和⊙M相交于A．B两点，AD为⊙M的直径，直线BD交⊙O于点C，点G为弧BD中点，连结AG分别交⊙O．BD于点E．F连结CE。
（Ⅰ）求证：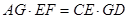
；
（Ⅱ）求证：
