设函数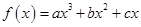 在区间
在区间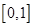 上是增函数,在区间
上是增函数,在区间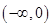 ,
,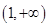 上是减函数,又
上是减函数,又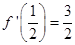
(1)求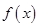 的解析式;
的解析式;
(2)若在区间
 上恒有
上恒有 成立,求
成立,求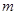 的取值范围
的取值范围
如图,已知四边形 是等腰梯形,
是等腰梯形, 、
、 分别是腰
分别是腰 、
、 的中点,
的中点, 、
、 是线段
是线段 上的两个点,且
上的两个点,且 ,下底是上底的2倍,若
,下底是上底的2倍,若 ,
, ,求
,求 .
.

在一家保险公司的董事会上,董事们就我国加入世界贸易组织(WTO)后公司的发展战略问题展开激烈讨论,其中一个议题是如何借鉴国外保险公司先进的管理经验,改进公司的管理模式.会议决定对推销员实行目标管理,即给推销员确定一个具体的销售目标.这个销售目标确定的是否合适,直接影响公司的经济效益.如果目标过高,多数推销员完不成任务,会使推销员失去信心;如果目标定得太低,将不利于挖掘推销员的工作潜力.下面一组数据是部分推销员的月销售额(单位:千元):
请根据这组样本数据提出使 %的职工能够完成销售指标的建议.
%的职工能够完成销售指标的建议.
如图, ,
, .求证:
.求证: .
.

 中,
中, 、
、 、
、 分别是
分别是 、
、 、
、 的中点,
的中点, 与
与 交于点
交于点 ,设
,设 ,
, .
.
(1)用 、
、 表示向量
表示向量 ;
;
(2)证明 、
、 、
、 三点在同一直线上,且
三点在同一直线上,且 .
.
已知点 ,
, ,
, 且
且 ,
, ,求点
,求点 ,
, 及向量
及向量 的坐标.
的坐标.