王老师编制了10道选择题,每题3分;对他所教的九年级(1)班和(2)班进行了检测如图(或表格)所示是从两个班分别随机抽取的10名学生的得分情况:
| 班级 |
平均数(分) |
中位数(分) |
众数(分) |
| (1)班 |
|
24 |
24 |
| (2)班 |
24 |
|
|
(1)请利用统计图中或统计表中所提供的信息,填充右表:
(2)把24分以上(含24分)记为“优秀”,若九(1)班为60名学生,请估算该班有多少名学生成绩优秀;
(3)请你先根据《九(2)班成绩统计表》中的数据绘制类似于九(1)班的统计图,再观察比较两个班的统计图中数据分布,你认为哪个班的学生成绩得分比较整齐些,并简述理由.九(2)班成绩统计表:
| 编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 成绩 |
24 |
21 |
30 |
21 |
27 |
15 |
27 |
21 |
24 |
30 |

如图,已知 为 的直径, ,点 和点 是 上关于直线 对称的两个点,连接 、 ,且 ,直线 和直线 相交于点 ,过点 作直线 与线段 的延长线相交于点 ,与直线 相交于点 ,且 .
(1)求证:直线 为 的切线;
(2)若点 为线段 上一点,连接 ,满足 ,
① ;
②求 的最大值.

如图已知函数 的图象与一次函数 的图象相交不同的点 、 ,过点 作 轴于点 ,连接 ,其中点 的横坐标为 , 的面积为2.
(1)求 的值及 时 的值;
(2)记 表示为不超过 的最大整数,例如: , ,设 ,若 ,求 值.
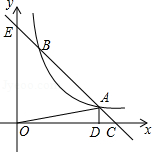
如图,在 和 的斜边分别为正方形的边 和 ,其中 .
(1)求证: ;
(2)线段 与线段 相交于 ,若 ,求 的值.

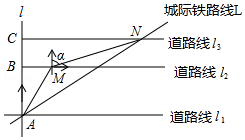
如图为某区域部分交通线路图,其中直线 ,直线 与直线 、 、 都垂直,垂足分别为点 、点 和点 ,(高速路右侧边缘), 上的点 位于点 的北偏东 方向上,且 千米, 上的点 位于点 的北偏东 方向上,且 , 千米,点 和点 是城际线 上的两个相邻的站点.
(1)求 和 之间的距离;
(2)若城际火车平均时速为150千米 小时,求市民小强乘坐城际火车从站点 到站点 需要多少小时?(结果用分数表示)
为提高公民法律意识,大力推进国家工作人员学法用法工作,今年年初某区组织本区900名教师参加“如法网”的法律知识考试,该区 学校参考教师的考试成绩绘制成如下统计图和统计表(满分100分,考试分数均为整数,其中最低分76分)
|
分数 |
人数 |
|
85.5以下 |
10 |
|
85.5以上 |
35 |
|
96.5以上 |
8 |
(1)求 学校参加本次考试的教师人数;
(2)若该区各学校的基本情况一致,试估计该区参考教师本次考试成绩在90.5分以下的人数;
(3)求 学校参考教师本次考试成绩 分之间的人数占该校参考人数的百分比.
