为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由.
下面的临界值表供参考:
(参考公式: ,其中
,其中 )
)
(本小题满分13分)已知函数 在
在 处取得极值.
处取得极值.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)若关于 的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围;
的取值范围;
(Ⅲ)证明:对任意的正整数 ,不等式
,不等式 都成立.
都成立.
(本小题满分13分) 已知椭圆E中心在原点,一个焦点为 ,离心率
,离心率
(Ⅰ)求椭圆E的方程;
(Ⅱ) 是长为
是长为 的椭圆E动弦,
的椭圆E动弦, 为坐标原点,求
为坐标原点,求 面积的最大值与最小值
面积的最大值与最小值
(本小题满分13分) 某生产流水线由于改进了设备,预计改进后第一年年产量的增长率为 ,以后每年的增长率是前一年的一半,设原来的产量是
,以后每年的增长率是前一年的一半,设原来的产量是
(Ⅰ) 写出改进设备后的第一年、第二年、第三年的产量,并写出第 年与第
年与第 年的产量之间的关系式
年的产量之间的关系式 ;
;
(Ⅱ) 由于设备不断老化,估计每年将损失年产量的 ,如此下去,以后每年的产量是否始终是逐年提高?若是,请给予证明;若不是,请说明从第几年起,产量将比上一年减少?
,如此下去,以后每年的产量是否始终是逐年提高?若是,请给予证明;若不是,请说明从第几年起,产量将比上一年减少?
(本小题满分12分)已知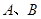 分别在射线
分别在射线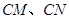 (不含端点
(不含端点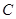 )上运动,
)上运动,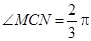 ,在
,在 中,角
中,角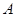 、
、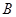 、
、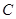 所对的边分别是
所对的边分别是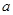 、
、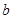 、
、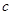 .
.
(Ⅰ)若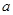 、
、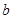 、
、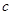 依次成等差数列,且公差为2.求
依次成等差数列,且公差为2.求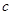 的值;
的值;
(Ⅱ)若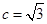 ,
,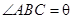 ,试用
,试用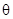 表示
表示 的周长,并求周长的最大值.
的周长,并求周长的最大值.