设甲、乙、丙三人进行围棋比赛,每局两人参加,没有平局。在一局比赛中,甲胜乙的概率为 ,甲胜丙的概率为
,甲胜丙的概率为 ,乙胜丙的概率为
,乙胜丙的概率为 。比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束。
。比赛顺序为:首先由甲和乙进行第一局的比赛,再由获胜者与未参加比赛的选手进行第二局的比赛,依此类推,在比赛中,有选手获胜满两局就取得比赛的胜利,比赛结束。
(1)求只进行了三局比赛,比赛就结束的概率;
(2)记从比赛开始到比赛结束所需比赛的局数为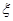 ,求
,求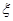 的概率分布列和数学期望
的概率分布列和数学期望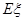 。
。
(本小题满分12分)一次数学测验,某班50名的成绩全部介于90分到140分之间.将成绩结果按如下方式分成五段:第一段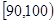 ,第二段
,第二段 ,……,第五段
,……,第五段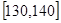 .按上述分段方法得到的频率分布直方图如图所示.
.按上述分段方法得到的频率分布直方图如图所示.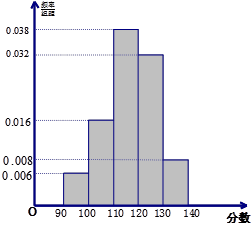
(Ⅰ)若成绩大于或等于100分且小于120分认为是良好的,求该校参赛学生在这次数学联赛中成绩良好的人数;
(Ⅱ)现将分数在[90,110)内同学分为第1组,在[110,120)内的分为第2组,在[120,140)内的分为第3组,然后从中随机抽取2人,用ξ表示这2人所在组数之差的绝对值,求ξ的分布列和期望.
(本小题满分14分)如图,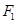 、
、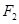 为椭圆
为椭圆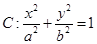 的左、右焦点,
的左、右焦点,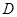 、
、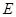 是椭圆的两个顶点,椭圆的离心率
是椭圆的两个顶点,椭圆的离心率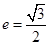 ,
,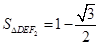 .若
.若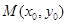 在椭圆
在椭圆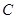 上,则点
上,则点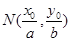 称为点
称为点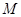 的一个“椭点”.直线
的一个“椭点”.直线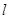 与椭圆交于
与椭圆交于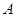 、
、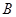 两点,
两点, 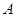 、
、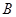 两点的“椭点”分别为
两点的“椭点”分别为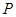 、
、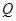 .
.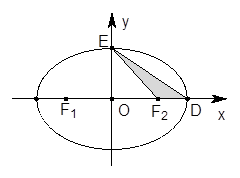
(Ⅰ)求椭圆的标准方程;
(Ⅱ)是否存在过左焦点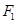 的直线
的直线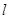 ,使得以
,使得以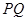 为直径的圆经过坐标原点?若存在,求出该直线方程,若不存在,是说明理由.
为直径的圆经过坐标原点?若存在,求出该直线方程,若不存在,是说明理由.
(本小题满分13分)设函数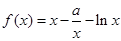 .
.
(Ⅰ)若函数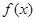 在定义域上为增函数,求实数
在定义域上为增函数,求实数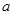 的取值范围;
的取值范围;
(Ⅱ)求函数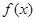 的极值点.
的极值点.
(本小题满分12分)已知数列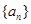 的前n项和是
的前n项和是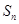 ,且
,且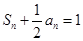 .
.
(Ⅰ)求数列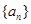 的通项公式;
的通项公式;
(Ⅱ)记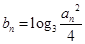 ,数列
,数列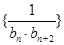 的前
的前 项和
项和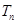 ,证明
,证明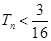 .
.
(本小题满分12分)如图1所示的梯形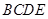 中,
中,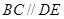 ,
, ,且
,且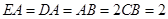 ,如图2,沿
,如图2,沿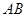 将四边形
将四边形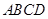 折起,使得面
折起,使得面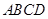 与面
与面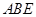 垂直,
垂直,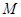 为
为 的中点.
的中点.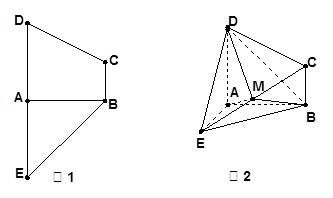
(Ⅰ)求证:平面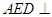 平面
平面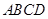
(Ⅱ)求证: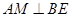 .
.