设平面三点A(1,0),B(0,1),C(2,5).
(1)求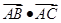 的值;
的值;
(2)求向量 与
与 的夹角的余弦值;
的夹角的余弦值;
(3)试求与 垂直的单位向量的坐标.
垂直的单位向量的坐标.
若椭圆 :
: 的离心率等于
的离心率等于 ,抛物线
,抛物线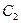 :
: 的焦点在椭圆的顶点上。
的焦点在椭圆的顶点上。
(1)求抛物线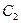 的方程;
的方程;
(2)求过点 的直线
的直线 与抛物线
与抛物线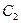 交
交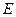 、
、 两点,又过
两点,又过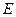 、
、 作抛物线
作抛物线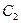 的切线
的切线 、
、 ,当
,当 时,求直线
时,求直线 的方程。
的方程。
如图,△ABC内接于圆O,AB是圆O的直径,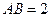 ,
,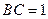 ,设AE与平面ABC所成的角为
,设AE与平面ABC所成的角为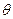 ,且
,且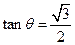 ,
,
四边形DCBE为平行四边形,DC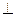 平面ABC.
平面ABC.
(1)求三棱锥C-ABE的体积;
(2)证明:平面ACD 平面ADE;
平面ADE;
(3)在CD上是否存在一点M,使得MO//平面ADE?证明你的结论.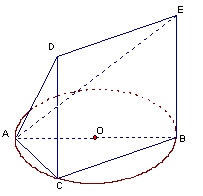
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:

(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅲ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求 的分布列及数学期望.
的分布列及数学期望.
已知函数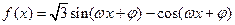 (
(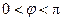 ,
, )为偶函数,且函数
)为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为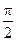 .
.
(1)求 的值;
的值;
(2)将函数 的图象向右平移
的图象向右平移 个单位后,纵坐标不变,得到函数
个单位后,纵坐标不变,得到函数 的
的
图象,求 的单调递减区间.
的单调递减区间.
已知函数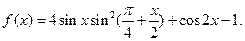
(1)设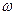 >0为常数,若
>0为常数,若 上是增函数,求
上是增函数,求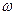 的取值范围;
的取值范围;
(2)设集合 若A
若A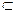 B恒成立,求实数
B恒成立,求实数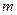 的取值范围
的取值范围