为了解学生身高情况,某校以10%的比例对全校700名学生按性
别进行分层抽样调查,测得身高情况的统计图如下: 

(1)估计该校男生的人数;
(2)估计该校学生身高在170~185㎝之间的概率;
(3)从样本中身高在165~180㎝之间的女生中任选2人,求至少有1人身高在170~180㎝之间的概率;
(本小题满分12分)如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,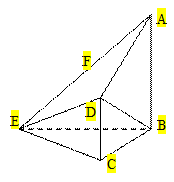 AB=BC=CE=2CD=2,∠BCE=1200,F为AE中点。
AB=BC=CE=2CD=2,∠BCE=1200,F为AE中点。
(Ⅰ) 求证:平面ADE⊥平面ABE ;
(Ⅱ)求二面角A—EB—D的大小的余弦值;
(Ⅲ)求点F到平面BDE的距离.
如右图所示,四边形ABCD内接于⊙O,AB=AD,过A点的切线交CB的延长线于E点.
求证:AB2=BE·CD.
 如右图所示,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M.
如右图所示,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M.
(1)求证:DC是⊙O的切线;
(2)求证:AM·MB=DF·DA.
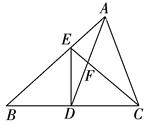 如右图,已知在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
如右图,已知在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
(1)求证:△ABC∽△FCD.
(2)若S△FCD=5,BC=10,求DE的长.
如右图所示,E为△ABC的边AC上一点,=,连结BE.
(1)若G为BE的中点,连结AG并延长交BC于D,求BD∶DC的值.
(2)若BG∶GE=2∶1,则BD∶DC的值将如何变化?
(3)若的值由改变为,G仍为BE中点,求BD∶DC.