 如右图所示,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M.
如右图所示,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M.
(1)求证:DC是⊙O的切线;
(2)求证:AM·MB=DF·DA.
(本题12分)口袋里放了12个大小完全一样的小球,其中3个是红色的,
4个是白色的,5个是蓝色的,现从袋中任意取出4个小球,求:
(1) 取出的小球的颜色至少是两种的概率;
(2) 取出的小球的颜色是三种的概率.
(本题12分)七个人排成两排照相,前排3人,后排4人.
(1) 求甲在前排,乙在后排的概率;
(2)求甲、乙在同一排且相邻的概率;
(3) 求甲、乙之间恰好有一人的概率.
(本题12分)已知 是定义在R上的函数, 且
是定义在R上的函数, 且 在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
在(-1,0)和(4,5)上有相同的单调性,在(0,2)和(4,5)上
有相反的单调性.
(1) 求 的值;
的值;
(2) 在函数 的图象上是否存在一点
的图象上是否存在一点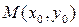 ,使得
,使得 在点
在点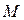 的
的
切线斜率为 ?若存在,求出点
?若存在,求出点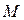 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
设函数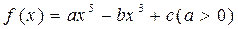 .
.
(1)若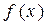 在
在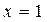 和
和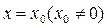 处有不同的极值,且极大值为4,
处有不同的极值,且极大值为4,
极小值为1,求 及实数
及实数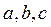 的值;
的值;
(2) 若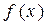 在
在 上单调递增且
上单调递增且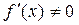 ,求
,求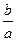 的最大值.
的最大值.
(本题10分)在等比数列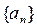 中,
中,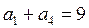 ,
,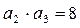 ,
,
求数列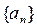 的前6项和
的前6项和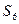 .
.