(本小题满分12分)
在等差数列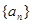 中,首项
中,首项 ,数列
,数列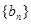 满足
满足
(I)求数列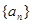 的通项公式;
的通项公式;
(II)求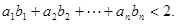
(本小题满分12分)
已知数列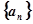 是首项为1的等差数列,且
是首项为1的等差数列,且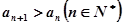 , 若
, 若
成等比数列.
(1)求数列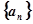 的通项公式;(2)设
的通项公式;(2)设 ,求数列
,求数列 的前
的前 项和
项和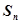 .
.
.(本小题满分12分)
已知函数 的最小正周期为
的最小正周期为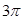 ,且当
,且当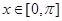 时,函数
时,函数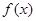 的最小值为0。
的最小值为0。
(I)求函数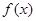 的表达式;
的表达式;
(II)在△ABC,若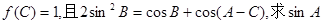 的值。
的值。
.(本小题满分14分)已知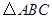 的顶点
的顶点 ,
,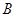 在椭圆
在椭圆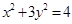 上,
上, 在直线
在直线 上,且
上,且 .
.
(1)当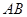 边通过坐标原点
边通过坐标原点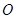 时,求
时,求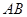 的长及
的长及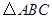 的面积;
的面积;
(2)当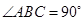 ,且斜边
,且斜边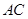 的长最大时,求
的长最大时,求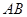 所在直线的方程.
所在直线的方程.
.(本小题满分12分)如图所示,矩形ABCD的边AB= ,BC=2,PA⊥平面ABCD,PA=2,现有数据: ①
,BC=2,PA⊥平面ABCD,PA=2,现有数据: ① ;②
;② ;③
;③ ;建立适当的空间直角坐标系,
;建立适当的空间直角坐标系,
(I)当BC边上存在点Q,使PQ⊥QD时, 可能取所给数据中的哪些值?请说明理由;
可能取所给数据中的哪些值?请说明理由;
(II)在满足(I)的条件下,若 取所给数据的最小值
取所给数据的最小值 时,这样的点Q有几个? 若沿BC方向依次记为
时,这样的点Q有几个? 若沿BC方向依次记为 ,试求二面角
,试求二面角 的大小.
的大小.