(本小题满分12分)
已知
用数学归纳法 证明:
证明:
观察下列式子: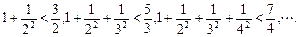 请归纳出关于n的一个不等式并加以证明.
请归纳出关于n的一个不等式并加以证明.
若两条曲线的极坐标方程分别为 与
与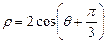 ,它们相交于
,它们相交于 两点,求线段
两点,求线段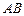 的长.
的长.
有甲、乙两个盒子,甲盒子中装有3个小球,乙盒子中装有5个小球,每次随机选取一个盒子并从中取出一个球。
(I)求当甲盒子中的球被取完时,乙盒子中恰剩下2个球的概率;
(Ⅱ)当第一次取完一个盒子中的球时,另一个盒子恰剩下 个球,求
个球,求 的分布列及期望
的分布列及期望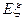 .
.
已知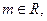 且复数z=(2+
且复数z=(2+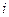 )
)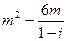

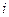 )在复平面内表示的点为A.
)在复平面内表示的点为A.
(1)当实数m取什么值时,复数z是纯虚数;
(2)当点A位于第二象限时,求实数m的取值范围.
已知一个四棱锥P—ABCD的三视图(正视图与侧视图为直角三角形,俯视图是带有一条对角形的正方形)如下,E是侧棱PC上的动点。
(1)求四棱锥P—ABCD的体积;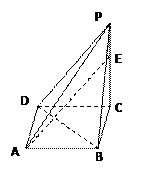 (2)是否不论点E 在何位置都有BD⊥AE,证明你的结论。
(2)是否不论点E 在何位置都有BD⊥AE,证明你的结论。
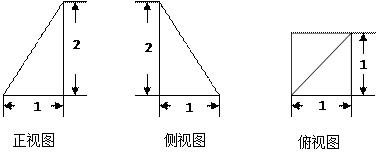 |