已知椭圆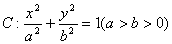 的左顶点
的左顶点 ,过右焦点
,过右焦点 且垂直于长轴的弦长为
且垂直于长轴的弦长为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若过点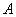 的直线
的直线 与椭圆交于点
与椭圆交于点 ,与
,与 轴交于点
轴交于点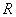 ,过原点与
,过原点与 平行的直线与椭圆交于点
平行的直线与椭圆交于点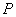 ,求证:
,求证: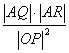 为定值.
为定值.
((本小题满分12分)
已知椭圆的中心为坐标原点O,焦点在x轴上,椭圆短半轴长为1,动点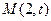
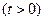 在直线
在直线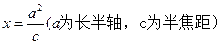 上。
上。
(1)求椭圆的标准方程
(2)求以OM为直径且被直线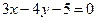 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;
(3)设F是椭圆的右焦点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值,并求出这个定值。
((本小题满分12分)
若图为一简单组合体,其底面ABCD为正方形,PD 平面ABCD,EC//PD,且PD=2EC。
平面ABCD,EC//PD,且PD=2EC。
(1)求证:BE//平面PDA;
(2)若N为线段PB的中点,求证:EN 平面PDB;
平面PDB;
(3)若 ,求平面PBE与平面ABCD所成的二面角的大小。
,求平面PBE与平面ABCD所成的二面角的大小。
(本小题满分12分)
为了解我区中学生的体质状况及城乡大学生的体质差异,对银川地区部分大学的学生进行了身高、体重和肺活量的抽样调查。现随机抽取100名学生,测得其身高情况如下表所示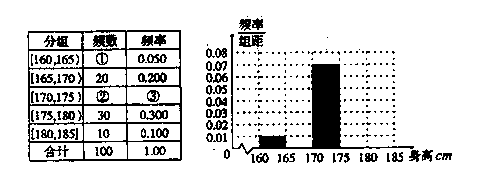
(1)请在频率分布表中的①、②、③位置填上相应的数据,并补全频率分布直方图,再根据频率分布直方图估计众数的值;
(2)若按身高分层抽样,抽取20人参加2011年庆元旦“步步高杯”全民健身运动其中有3名学生参加越野比赛,记这3名学生中“身高低于170Ccm”的人数为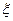 ,求
,求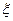 的分布列及期望。
的分布列及期望。
(本小题满分12分)
已知sin-2cos=0.
(1)求tanx的值;
(2)求的值.
已知函数
 是奇函数.
是奇函数.
(1)求实数 的值;
的值;
(2)判断函数 在
在 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)当 时,函数
时,函数 的值域是
的值域是 ,求实数
,求实数 与
与 的值
的值