已知在△ABC中, a、b、c分别为角A、B、C的对边,且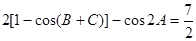
(1)若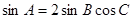 ,试判断△ABC的形状;
,试判断△ABC的形状;
(2)若a=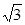 ,b+c=3,求b和c的值.
,b+c=3,求b和c的值.
“依法纳税是每个公民应尽的义务”,《中华人民共和国个人所得税法》第十四条中有个人所得税税率表(工资、薪金所得适用):
| 级数 |
全月应纳税所得额 |
税率(%) |
| 1 |
不超过500元部分 |
5 |
| 2 |
超过500元至2 000元部分 |
10 |
| 3 |
超过2 000元至5 000元部分 |
15 |
| 4 |
超过5 000元至20 000元部分 |
20 |
| …… |
…… |
目前,上表中“全月应纳税所得额”是从月工资、薪金收入中减去1 600元后的余额,例如某人月工资、薪金收入为1 820元,减去1 600元后,应纳税所得额就是220元,应缴纳个人所得税11元.编写一个程序,输入某人月工资、薪金,输出这个人应缴纳的个人所得税(只计算到级数为3时).
铁路运输托运行李,从甲地到乙地,规定每张客票托运费计算方法是行李质量不超过50 kg时按0.25元/kg;超过50 kg而不超过100 kg时,其超过部分按0.35元/kg;超过100 kg时,其超过部分按0.45元/kg.编写程序,输入行李质量,计算并输出托运的费用.
程序框图如图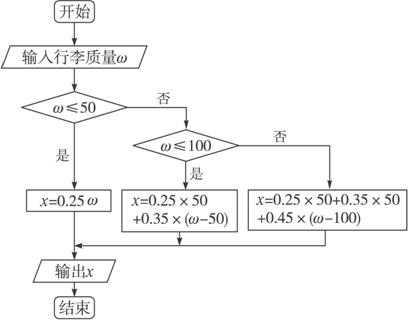
相传古代的印度国王要奖赏国际象棋的发明者,问他需要什么.发明者说:陛下,在国际象棋的第一个格子里面放1粒麦子,在第二个格子里面放2粒麦子,第三个格子放4粒麦子,以后每个格子中的麦粒数都是它前一个格子中麦粒数的二倍,依此类推(国际象棋棋盘共有64个格子).请将这些麦子赏给我,我将感激不尽.国王想这还不容易,就让人扛了一袋小麦,但不到一会儿就没了,最后一算结果,全印度一年生产的粮食也不够.国王很奇怪,小小的“棋盘”,不足100个格子,如此计算怎么能放这么多麦子?试用程序框图表示一下算法过程.
如图所示,有一城市,市区为半径为15 km的圆形区域,近郊区为距中心15—25 km范围内的环形地带,距中心25 km以外的为远郊区.市区地价每公顷100万元,近郊区地价每公顷60万元,远郊区地价为每公顷20万元,输入某一点的坐标为(x,y),求该点的地价.请设计出相应的程序框图. 
设计一个计算1+2+…+100的值的算法,用程序框图表示.