如图,正方形ABCD中,O是对角线AC、BD的交点,过点O作OE⊥OF,分别交AB、BC于E、F.
(1)求证:△OEF是等腰直角三角形.
(2)若AE=4,CF=3,求EF的长.
为了加强食品安全管理,有关部门对某大型超市的甲、乙两种品牌食用油共抽
18瓶进行检测,检测结果分成“优秀”、“合格”、“不合格”三个等级,数据处理后制成以
下折线统计图和扇形统计图.
⑴甲、乙两种品牌食用油各被抽取了多少瓶用于检测?
⑵在该超市购买一瓶乙品牌食用油,请估计能买到“优秀”等级的概率是多少?
如图l0.在平面直角坐标系xoy中,AB在x轴上,AB=10.以AB为直径的⊙O’与y轴正半轴交于点C.连接BC,AC。CD是⊙O’的切线.AD⊥CD于点D,tan∠CAD=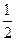 ,抛物线
,抛物线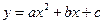 过A、B、C三点。
过A、B、C三点。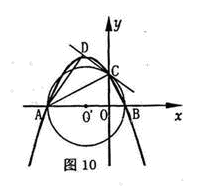
(1)求证:∠CAD=∠CAB;
(2)①求抛物线的解析式;
②判断抛物线的顶点E是否在直线CD上.并说明理由:
(3)在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在.请说明理由.
如图9,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE, PE交边BC于点F.连接BE、DF。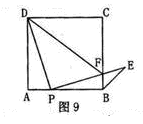
(1)求证:∠ADP=∠EPB;
(2)求∠CBE的度数;
(3)当 的值等于多少时.△PFD∽△BFP?并说明理由.
的值等于多少时.△PFD∽△BFP?并说明理由.
为发展旅游经济.我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人.非节假日打4折售票.节假日按团队人数分段定价售票,即m人以下(含m人)的团队接原价售票;超过m人的团队.其中m人仍按原价售票.超过m人部分的游客打b折售票.设某旅游团人数为x人.非节假日购票款为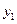 (元),节假日购票款为
(元),节假日购票款为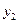 (元).
(元).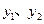 与x之间的函数图象如图8所示.
与x之间的函数图象如图8所示.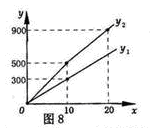
(1)观察图象可知:a=______;b=______;m=______;
(2)直接写出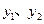 与x之间的函数关系式:
与x之间的函数关系式:
(3)某旅行杜导游王娜于5月1日带A团.5月20日(非节假日)带B团都到该景区旅游.共付门票款1900元.A,B两个团队合计50人,求A,B两个团队各有多少人?
如图7.在⊙O中.弦BC垂直于半径OA.垂足为E.D是优弧 上一点.连接BD.AD.OC,∠ADB=30°.
上一点.连接BD.AD.OC,∠ADB=30°.
(1)求∠AOC的度教;
(2)若弦BC=6cm.求图中阴影部分的面积.