已知数列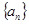 满足:
满足: ,
, 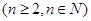 ,
, ,前
,前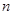 项和为
项和为 的数列
的数列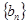 满足:
满足: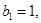
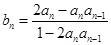
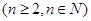 ,又
,又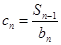
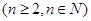 。
。
(1)求数列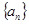 的通项公式;
的通项公式;
(2)证明: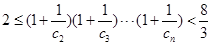
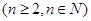 ;
;
设Sn为等差数列{a n}的前n项和,已知a 9 =-2,S 8 =2.
(1)求首项a1和公差d的值;
(2)当n为何值时,Sn最大?并求出Sn的最大值.
设
(1)当 ,求
,求 的取值范围;
的取值范围;
(2)若对任意 ,
, 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
极坐标系与直角坐标系xOy有相同的长度单位,以原点D为极点,以x轴正半轴为极轴,曲线Cl的极坐标方程为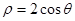 ,曲线C2的参数方程为
,曲线C2的参数方程为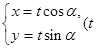 为参数)。
为参数)。
(1)当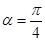 时,求曲线Cl与C2公共点的直角坐标;
时,求曲线Cl与C2公共点的直角坐标;
(2)若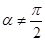 ,当
,当 变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.
变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.
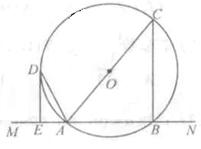
如图,直线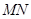 交圆
交圆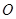 于
于 两点,
两点,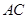 是直径,
是直径,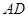 平分
平分 ,交圆
,交圆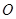 于点
于点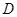 , 过
, 过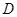 作
作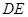 丄
丄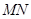 于
于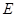 .
.
(1)求证: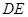 是圆
是圆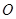 的切线;
的切线;
(2)若 ,求
,求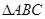 的面积
的面积
设函数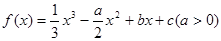 ,曲线
,曲线 在点
在点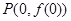 处的切线方程为
处的切线方程为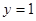
(1)确定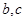 的值
的值
(2)若过点(0,2)可做曲线 的三条不同切线,求
的三条不同切线,求 的取值范围
的取值范围
(3)设曲线 在点
在点 处的切线都过点(0,2),证明:当
处的切线都过点(0,2),证明:当 时,
时,