在数列{ }中,
}中, ,且
,且
 ,
,
(1)求 的值;
的值;
(2)猜测数列{ }的通项公式,并用数学归纳法证明。
}的通项公式,并用数学归纳法证明。
在数列 中,已知
中,已知 .
.
(1)求数列 、
、 的通项公式;
的通项公式;
(2)设数列 满足
满足 ,求
,求 的前n项和
的前n项和
( 12分)如图,在多面体 中,
中, 面
面 ,
, ,且
,且 ,
,
 为
为 中点。
中点。
(1)求证: 平面
平面 ;
;
(2)求平面 和平面
和平面 所成的锐二面角的余弦值。
所成的锐二面角的余弦值。
已知函数
(1)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(2)设 的内角A、B、C的对边分别为
的内角A、B、C的对边分别为 ,且
,且 ,若向量
,若向量 与向量
与向量 共线,求
共线,求 的值。
的值。
(本小题满分12分)若对于正整数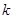 、
、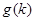 表示
表示
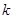 的最大奇数因数,
的最大奇数因数, 例如
例如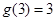 ,
,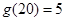 ,并且
,并且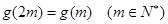 ,设
,设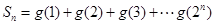
(1)求S1、S2、S3;
(2)求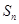 ;
;
(3)设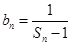 ,求证数列
,求证数列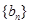 的前
的前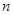 顶和
顶和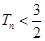 .
.
(本小题满分12分)中心在原点,焦点在x轴上的椭圆C上的点到焦点距离的最大值为3,最小值为1.
(1)求椭圆C的方程;
(2)若直线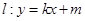 与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求该定点的坐标.
与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求该定点的坐标.