某项竞赛分别为初赛、复赛、决赛三个阶段进行,每个阶段选手要回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是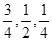 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在竞赛中回答问题的个数为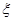 ,求
,求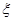 的分布列、数学期望和方差.
的分布列、数学期望和方差.
若 ,
, 是第四象限角,求
是第四象限角,求 的值.
的值.
为了参加奥运会,对自行车运动员甲、乙两人在相同的条件下进行了6次测试,测得他们的最大速度的数据如表所示:
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
(1)分别求甲、乙两运动员最大速度
的平均数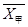 ,
,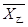 及方差
及方差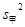 ,
, ;
;
(2)根据(1)所得数据阐明:谁参加这项重大比赛更合适.
(本小题满分14分)已知函数 .
.
(Ⅰ)若函数 为偶函数,求
为偶函数,求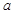 的值;
的值;
(Ⅱ)若 ,求函数
,求函数 的单调递增区间;
的单调递增区间;
(Ⅲ)当 时,若对任意的
时,若对任意的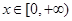 ,不等式
,不等式 恒成立,求实数
恒成立,求实数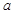 的取值范围.
的取值范围.
(本小题满分14分)已知半径为2,圆心在直线 上的圆C.
上的圆C.
(Ⅰ)当圆C经过点A(2,2)且与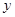 轴相切时,求圆C的方程;
轴相切时,求圆C的方程;
(Ⅱ)已知E(1,1),F(1,-3),若圆C上存在点Q,使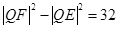 ,求圆心的横坐标
,求圆心的横坐标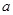 的取值范围.
的取值范围.
(本小题满分14分)如图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.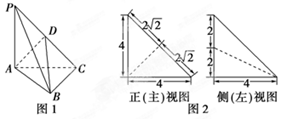
(1)证明:AD⊥平面PBC;
(2)求三棱锥D-ABC的体积;