已知抛物线y=ax2+bx+c与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正半轴上,点C在y轴的正半轴上,线段OB、OC的长(OB<OC)是方程x2-10x+16=0的两个根,且抛物线的对称轴是直线x=-2.
(1)求此抛物线的解析式;
(2)连接AC、BC,若点E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连接CE,设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式,并写出自变量m的取值范围;
(3)在(2)的基础上试说明S是否存在最大值,若存在,请求出S的最大值,并求出此时点E的坐标,判断此时△BCE的形状;若不存在,请说明理由。
某地区有城区居民和农村居民共80万人.某机构准备采用抽取样本的方法调查该地区居民“获取信息的最主要途径”.
(1)该机构设计了以下三种调查方案:
方案一:随机抽取部分城区居民进行调查;
方案二:随机抽取部分农村居民进行调查;
方案三:随机抽取部分城区居民和部分农村居民进行调查.
其中最具有代表性的一个方案是 ;
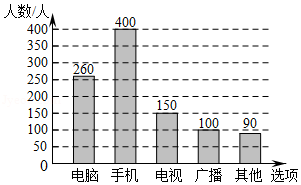
(2)该机构采用了最具有代表性的调查方案进行调查.供选择的选项有:电脑、手机、电视、广播、其他,共五个选项.每位被调查居民只选择一个选项.现根据调查结果绘制如下统计图,请根据统计图回答下列问题:
①这次接受调查的居民人数为 人;
②统计图中人数最多的选项为 ;
③请你估计该地区居民和农村居民将“电脑和手机”作为“获取信息的最主要途径”的总人数.
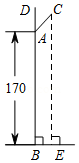
墙壁及淋浴花洒截面如图所示.已知花洒底座 与地面的距离 为 ,花洒 的长为 ,与墙壁的夹角 为 .求花洒顶端 到地面的距离 (结果精确到 .(参考数据: , ,
问题解决
糖葫芦一般是用竹签串上山楂,再蘸以冰糖制作而成.现将一些山楂分别串在若干根竹签上.如果每根竹签串5个山楂,还剩余4个山楂;如果每根竹签串8个山楂,还剩余7根竹签.这些竹签有多少根?山楂有多少个?
反思归纳
现有 根竹签, 个山楂.若每根竹签串 个山楂,还剩余 个山楂,则下列等式成立的是 (填写序号).
(1) ;(2) ;(3) .

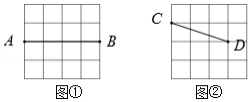
图①,图②均为 的正方形网格,每个小正方形的顶点称为格点.在图①中已画出线段 ,在图②中已画出线段 ,其中 、 、 、 均为格点,按下列要求画图:
(1)在图①中,以 为对角线画一个菱形 ,且 , 为格点;
(2)在图②中,以 为对角线画一个对边不相等的四边形 ,且 , 为格点, .
如图,在 中,点 在边 上,以 为圆心, 长为半径画弧,交边 于点 ,连接 、 .求证: .
