如图(1), 是等腰直角三角形,其中
是等腰直角三角形,其中 ,
, 分别为
分别为 的中点,将
的中点,将 沿
沿 折起,点
折起,点 的位置变为点
的位置变为点 ,已知点
,已知点 在平面
在平面 上的射影
上的射影 为
为 的中点,如图(2)所示.
的中点,如图(2)所示.
(1)求证: ;
;
(2)求三棱锥 的体积.
的体积.
解答题
22.如图: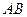 是⊙
是⊙ 的直径,
的直径,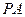 垂直于⊙
垂直于⊙ 所在的平面,
所在的平面, 是圆周上不同于
是圆周上不同于 的任意一点,求证:平面
的任意一点,求证:平面 。
。
已知抛物线C: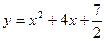 , 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线。
, 过抛物线C上点M且与M处的切线垂直的直线称为抛物线C在点M的法线。
⑴若抛物线C在点M的法线的斜率为 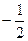 ,求点M的坐标
,求点M的坐标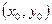 ;
;
⑵设P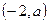 为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P。若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由。
为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P。若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由。
椭圆E的中心在原点O,焦点在x轴上,离心率e=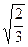 ,过点C(-1,0)的直线
,过点C(-1,0)的直线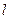 交椭圆于A,B两点,且满足
交椭圆于A,B两点,且满足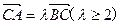 ,
, 为常数。
为常数。
(1)当直线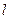 的斜率k=1且
的斜率k=1且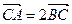 时,求三角形OAB的面积.
时,求三角形OAB的面积.
(2)当三角形OAB的面积取得最大值时,求椭圆E的方程.
如图,在四棱 锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。
锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点。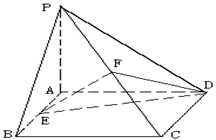
⑴求证:CD⊥PD;
⑵求证:EF∥平面PAD;
⑶若直线EF⊥平面PCD,求平面PCD与平面ABCD所成二面角的大小
设函数 ,其中向量
,其中向量
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)在ΔABC中,角A、B、C所对的边分别为a、b、c,若 ,且
,且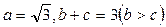 ,求
,求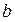 与
与 的值。
的值。