一般来说,一个人脚掌越长,他的身高就越高。现对10名成年人的脚掌长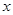 与身高
与身高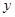 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为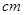 )作为样本如下表所示.
)作为样本如下表所示.
(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,作出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程 ;
;
(2)若某人的脚掌长为 ,试估计此人的身高;
,试估计此人的身高;
(3)在样本中,从身高180cm以上的4人中随机抽取2人作进一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率.
(参考数据: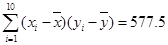 ,
,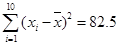 ,
,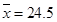 ,
,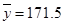 )
)
(12分)如图,在四棱锥 中,
中,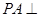 底面
底面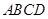 ,
,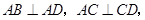
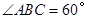 ,
,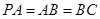 ,
, 是
是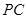 的中点.
的中点.
(Ⅰ)求 和平面
和平面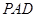 所成的角的大小;
所成的角的大小;
(Ⅱ)证明 平面
平面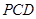 ;
;
(Ⅲ)求二面角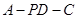 的正弦值.
的正弦值.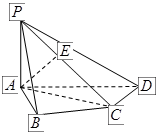
(12分)已知 :
: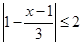 ,
,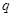 :
: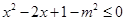 (
( ).若“非
).若“非 ”是“非
”是“非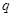 ”的必要而不充分条件,求实数
”的必要而不充分条件,求实数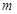 的取值范围.
的取值范围.
(12分)在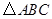 中,已知内角
中,已知内角 ,边
,边 .设内角
.设内角 ,周长为
,周长为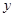 .
.
(1)求函数 的解析式和定义域
的解析式和定义域
(2)求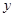 的最大值
的最大值
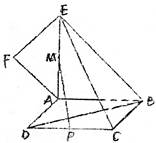
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是地面边长的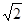 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P-AC-D的大小
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由。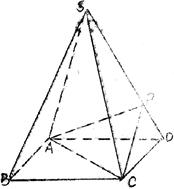
.如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=40°
(1)求证:EF⊥平面BCE;
(2)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE
(3)求二面角F—BD—A的大小。