现有8名奥运会志愿者,其中志愿者 通晓日语,
通晓日语, 通晓俄语,
通晓俄语,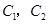 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(Ⅰ)求 被选中的概率;
被选中的概率;
(Ⅱ)求 和
和 不全被选中的概率.
不全被选中的概率.
如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以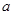 表示.已知甲、乙两个小组的数学成绩的平均分相同.
表示.已知甲、乙两个小组的数学成绩的平均分相同.
(1)求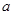 的值;
的值;
(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,求这两名同学数学成绩之差的绝对值为3的概率.
(注:方差 ,其中
,其中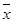 为
为 ,
,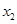 ,…,
,…, 的平均数)
的平均数)
已知函数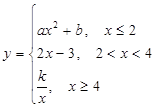 的图象如图所示.
的图象如图所示.
(1)求函数的解析式;
(2)完成下面的程序,并根据程序画出其程序框图.
INPUT“x=”;x
IF ①THEN
IF ②THEN
y=2*x-3
ELSE
y=k/x
END IF
ELSE
y=a*x^2+b
END IF
PRINT “y=”;y
END
已知一扇形的圆心角为 ,所在圆的半径为R,若扇形的周长为40cm,当它的圆心角
,所在圆的半径为R,若扇形的周长为40cm,当它的圆心角 为多少弧度时,该扇形的面积最大?最大面积为多少?
为多少弧度时,该扇形的面积最大?最大面积为多少?
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
(1)求证:FB=FC;
(2)求证:FB2=FA·FD;
(3)若AB是△ABC外接圆的直径,∠EAC=120°,BC=6 cm,求AD的长.