设
求 及
及 的单调区间
的单调区间
设 ,
,
 两点连线的斜率为
两点连线的斜率为 ,问是否存在常数
,问是否存在常数 ,且
,且 ,当
,当 时有
时有 ,当
,当 时有
时有 ;若存在,求出
;若存在,求出 ,并证明之,若不存在说明理由.
,并证明之,若不存在说明理由.
甲、乙两个箱子中装有大小相同的小球,甲箱中有2个红球和2个黑球,乙箱中装有2个黑球和3个红球,现从甲箱和乙箱中各取一个小球并且交换。
(1)求交换后甲箱中刚好有两个黑球的概率。
(2)设交换后甲箱中黑球的个数为 ,求
,求 的分布列和数学期望。
的分布列和数学期望。
已知参赛号码为1~4号的四名射箭运动员参加射箭比赛。
(1)通过抽签将他们安排到1~4号靶位,试求恰有一名运动员所抽靶位号与其参赛号码相同的概率;
(2)记1号,2号射箭运动员,射箭的环数为 (
( 所有取值为0,1,2,3...,10)。
所有取值为0,1,2,3...,10)。
根据教练员提供的资料,其概率分布如下表:
 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
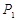 |
0 |
0 |
0 |
0 |
0.06 |
0.04 |
0.06 |
0.3 |
0.2 |
0.3 |
0.04 |
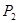 |
0 |
0 |
0 |
0 |
0.04 |
0.05 |
0.05 |
0.2 |
0.32 |
0.32 |
0.02 |
①若1,2号运动员各射箭一次,求两人中至少有一人命中8环的概率;
②判断1号,2号射箭运动员谁射箭的水平高?并说明理由.
某种家用电器每台的销售利润与该电器的无故障使用时间有关,每台这种家用电器若无故障使用时间不超过一年,则销售利润为0元,若无故障使用时间超过一年不超过三年,则销售利润为100元;若无故障使用时间超过三年,则销售利润为200元。已知每台该种电器的无故障使用时间不超过一年的概率为 无故障使用时间超过一年不超过三年的概率为
无故障使用时间超过一年不超过三年的概率为
(I)求销售两台这种家用电器的销售利润总和为400元的概率;
(II)求销售三台这种家用电器的销售利润总和为300元的概率;
北京的高考数学试卷中共有8道选择题,每个选择题都给了4个选项(其中有且仅有一个选项是正确的).评分标准规定:每题只选1项,答对得5分,不答或答错得0分.某考生每道题都给出了答案,已确定有4道题的答案是正确的,而其余的题中,有两道题每题都可判断其有两个选项是错误的,有一道题可以判断其一个选项是错误的,还有一道题因不理解题意只能乱猜.对于这8道选择题,试求:
(Ⅰ) 该考生得分为40分的概率;
(Ⅱ) 该考生所得分数 的分布列及数学期望
的分布列及数学期望 .
.
如图, 在矩形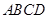 中,点
中,点 分别在线段
分别在线段 上,
上, .沿直线
.沿直线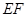 将
将  翻折成
翻折成 ,使平面
,使平面 .
.
(Ⅰ)求二面角 的余弦值;
的余弦值;
(Ⅱ)点 分别在线段
分别在线段 上,若沿直线
上,若沿直线 将四边形
将四边形 向上翻折,使
向上翻折,使 与
与 重合,求线段
重合,求线段 的长。
的长。