已知一个几何体的三视图如图所示。(1)求此几何体的表面积;(2)如果点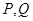 在正视图中所示位置:
在正视图中所示位置: 为所在线段中点,
为所在线段中点, 为顶点,求在几何体表面上,从
为顶点,求在几何体表面上,从 点到
点到 点的最短路径的长。
点的最短路径的长。
(本小题满分10分)
已知向量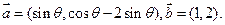
(1)若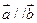 ,求
,求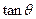 的值;
的值;
(2)若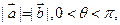 求
求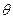 的值。
的值。
((本题16分)
(1)用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域用不同颜色鲜花,问共有多少种不同的摆放方案?
(2)用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图二所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域使用不同颜色鲜花.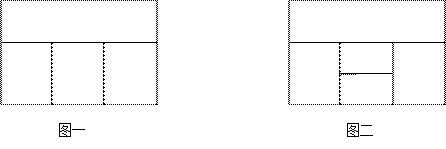
①求恰有两个区域用红色鲜花的概率;
②记花圃中红色鲜花区域的块数为S,求它的分布列及其数学期望E(S).
((本题16分)
已知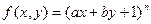 (常数
(常数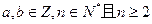 )
)
(1)若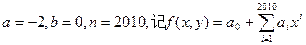 求:①
求:①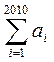 ;②
;②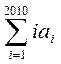
(2)若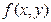 展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。
展开式中不含x的项的系数的绝对值之和为729,不含y项的系数的绝对值之和为64,求n的所有可能值。
((本题15分)
两个人射击,甲射击一次中靶概率是 ,乙射击一次中靶概率是
,乙射击一次中靶概率是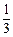 ,
,
(1)两人各射击一次,中靶至少一次就算完成目标,则完成目标概率是多少?
(2)两人各射击2次,中靶至少3次就算完成目标,则完成目标的概率是多少?
(3)两人各射击5次,是否有99%的把握断定他们至少中靶一次?
((本题15分)
在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1)。设k为非零实数,矩阵M=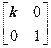 ,N=
,N=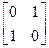 ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,
(1)求k的值。
(2)判断变换MN是否可逆,如果可逆,求矩阵MN的逆矩阵;如不可逆,说明理由.