如图,在底面是直角梯形的四棱锥S-ABCD中,
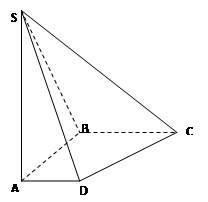
(1)求四棱锥S-ABCD的体积;
(2)求证:
(3)求SC与底面ABCD所成角的正切值。
(本小题共13分) 如图,在三棱锥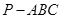 中,
中,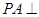 底面ABC
底面ABC ,点
,点 、
、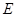 分别在棱
分别在棱 上,且
上,且
(Ⅰ)求证: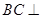 平面
平面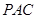 ;
;
(Ⅱ)当 为
为 的中点时,求
的中点时,求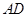 与平面
与平面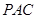 所成角的大小的余弦值;
所成角的大小的余弦值;
(Ⅲ)是否存在点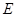 ,使得二面角
,使得二面角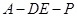 为直二面角?并说明理由.
为直二面角?并说明理由.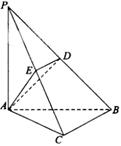
A处一缉私艇发现在北偏东45°方向,距离12 n mile的海面C处有一走私船正以10 n mile/h的速度沿东偏南15°方向逃窜.缉私艇的速度为14 n mile/h,若要在最短的时间内追上该走私船,缉私艇应沿北偏东45°+α的方向去追,求追击所需的时间和α角的正弦值.
(本小题满分13分)
已知函数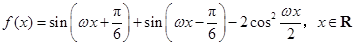 (其中
(其中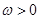 )
)
(I)求函数 的值域;(II)若对任意的
的值域;(II)若对任意的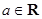 ,函数
,函数 ,
,
的图象与直线 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定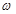 的值(不必证明),并求函数
的值(不必证明),并求函数 的单调增区间
的单调增区间
(本小题满分13分)数列 上,
上,
(1)求数列 的通项公式;(2)若
的通项公式;(2)若
(本小题满分14分)已知函数 ;
;
(1)若 ,求
,求 的值域;(2)在(1)的条件下,判断
的值域;(2)在(1)的条件下,判断 的单调性;(3)当
的单调性;(3)当 时
时 有意义求实
有意义求实 的范围。
的范围。