为了防控甲型H7N9流感,某校积极进行校园环境消毒,购买了甲、乙两种消毒液共100瓶,其中甲种6元/瓶,乙种9元/瓶.
(1)如果购买这两种消毒液共用780元,求甲、乙两种消毒液各购买多少瓶?
(2)该校准备再次购买这两种消毒液(不包括已购买的100瓶),使乙种瓶数是甲种瓶数的2倍,且这次所需费用不多于1200元(不包括之前的780元),求甲种消毒液最多能再购买多少瓶?
计算:1+2+3+4-5-6+7+8-9-10+11+12-13-14+15+.....+1992-1993-1994+1995
出租司机小张某天下午的营运全是在到西走向的大街上进行的,若规定向东为正,向西为负,他这天下午行车里程(单位:千米)记录如下: +8,-3,+15,-10,-13,+3,-15,+11,-12
(1)将最后一名乘客送到目的地时,小张距下午出车点的距离是多少千米?
(2)若汽车耗油量为0.08升/千米,这天下午汽车共耗油多少升?
10名学生体检测体重,以50千克为基准,超过的数记为正,不足的数记为负,称得结果如下(单位:千克):2, 3, -7.5,-3, 5, -8, 3.5, 4.5, 8, -1.5
这10名学生的总体重为多少?10名学生的平均体重为多少?
-55起逐次加上1,得到一连串的数:-54,-53,-52,……,
(1)第100个整数是什么?(2)求这100个整数的和。
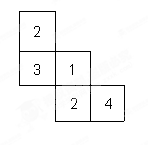
如图,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数。请你画出它的主视图与左视图。