在如图所示的几何体中,四边形 是菱形,
是菱形,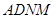 是矩形,平面
是矩形,平面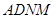 ⊥平面
⊥平面 ,
,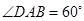 ,
,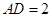 ,
,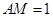 ,
,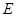 是
是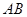 的中点.
的中点.
(Ⅰ) 求证: //平面
//平面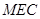 ;
;
(Ⅱ) 在线段 上是否存在点
上是否存在点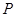 ,使二面角
,使二面角 的大小为
的大小为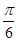 ?若存在,求出
?若存在,求出 的长
的长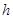 ;若不存在,请说明理由.
;若不存在,请说明理由.
如图1,四棱锥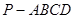 中,
中, 底面
底面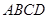 ,面
,面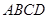 是直角梯形,
是直角梯形,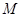 为侧棱
为侧棱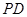 上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
(1)证明: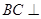 平面
平面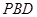 ;
;
(2)线段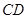 上是否存在点
上是否存在点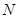 ,使
,使 与
与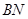 所成角的余弦值为
所成角的余弦值为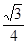 ?若存在,找到所有符合要求的点
?若存在,找到所有符合要求的点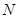 ,并求
,并求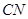 的长;若不存在,说明理由.
的长;若不存在,说明理由.
已知函数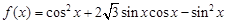
(1)求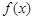 的最小正周期和值域;
的最小正周期和值域;
(2)在 中,角
中,角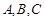 所对的边分别是
所对的边分别是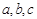 ,若
,若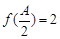 且
且 ,试判断
,试判断 的形状.
的形状.
袋中装有大小相同的2个白球和3个黑球.
(1)采取放回抽样方式,从中依次摸出两个球,求两球颜色不同的概率;
(2)采取不放回抽样方式,从中依次摸出两个球,记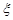 为摸出两球中白球的个数,
为摸出两球中白球的个数,
求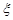 的期望.
的期望.
已知函数 ,
, ,其中
,其中 .
.
(1)若 是函数
是函数 的极值点,求实数
的极值点,求实数 的值;
的值;
(2)若对任意的 (
( 为自然对数的底数)都有
为自然对数的底数)都有 ≥
≥ 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知函数 ,曲线
,曲线 在点
在点 处的切线为
处的切线为 ,若
,若 时,
时, 有极值.
有极值.
(1)求 的值;
的值;
(2)求 在
在 上的最大值和最小值.
上的最大值和最小值.