函数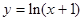
(1)若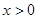 ,证明
,证明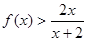 ;
;
(2)若不等式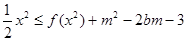 时
时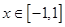 和
和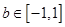 都恒成立,求实数
都恒成立,求实数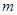 的取值范围。
的取值范围。
(本小题共14分)
三棱柱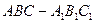 中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
, ,
,  分别是
分别是 ,
,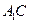 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: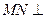 平面
平面 ;
;
(Ⅲ)求三棱锥
 的体积.
的体积.
(本小题共13分)
为了调查某厂2000名工人生产某种产品的能力,随机抽查了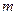 位工人某天生产该产品的数量,产品数量的分组区间为
位工人某天生产该产品的数量,产品数量的分组区间为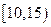 ,
, ,
,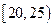 ,
,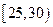 ,
,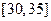 ,频率分布直方图如图所示.已知生产的产品数量在
,频率分布直方图如图所示.已知生产的产品数量在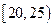 之间的工人有6位.
之间的工人有6位.
(Ⅰ)求 ;
;
(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训,则这2位工
人不在同一组的概率是多少?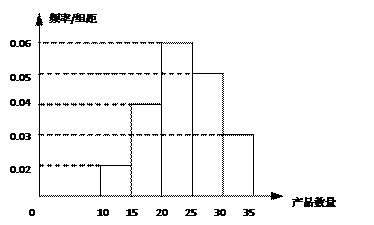
(本小题共12分)
在 中,角
中,角 所对的边分别为
所对的边分别为 ,满足
,满足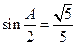 ,且
,且 的面积为
的面积为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若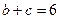 ,求
,求 的值.
的值.
(本小题满分14分)
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列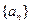 是调和数列,对于各项都是正数的数列
是调和数列,对于各项都是正数的数列 ,满足
,满足
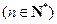 .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)把数列 中所有项按如图所示的规律排成一个三角形数表,
中所有项按如图所示的规律排成一个三角形数表,
当 时,求第
时,求第 行各数的和;
行各数的和;
(Ⅲ)对于(Ⅱ)中的数列 ,若数列
,若数列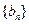 满足
满足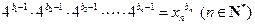 ,求证:数列
,求证:数列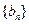 为等差数列.
为等差数列.
(本小题满分13分)
已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为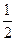 ,且经过点
,且经过点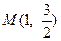 ,过点
,过点 的直线
的直线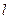 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点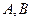 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)是否存直线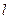 ,满足
,满足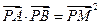 ?若存在,求出直线
?若存在,求出直线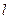 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.