某工厂有甲、乙两个生产小组，每个小组各有四名工人，某天该厂每位工人的生产情况如下表．
| |
员工号 |
1 |
2 |
3 |
4 |
| 甲组 |
件数 |
9 |
11 |
1l |
9 |
| |
员工号 |
1 |
2 |
3 |
4 |
| 乙组 |
件数 |
9 |
8 |
10 |
9 |
(1)用茎叶图表示两组的生产情况；
(2)求乙组员工生产件数的平均数和方差；
(3)分别从甲、乙两组中随机选取一名员工的生产件数，求这两名员工的生产总件数为19的概率．
（注：方差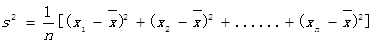
，其中
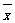为x1，x2， ，xn的平均数）
（本小题满分12分）
已知定义在R上的函数
的图像关于原点对称，且x=1
时，f(x)取极小值
．
(Ⅰ)求f(x)的解析式；
(Ⅱ)当x∈[-1，1]时，图像上是否存在两点，使得在此两点处的切线互相垂直?证明你的结
论．
（本小题满分12分）
设数列
为等差数列，且
，
，数列
的前
项和为
，
（Ⅰ）求数列
的通项公式；
（Ⅱ）若
，求数列
的前项和
.
（本小题满分12分）
如图所示，在正三棱柱
中，底面边长为
，侧棱长为
，
是棱
的中点.
|
(Ⅰ)求证:
平面
；
的大小；
到平面的距离.
（本小题满分12分）
将一个各个面上均涂有颜色的正方体锯成27个同样大小的小正方体
（Ⅰ）从这些小正方体中任取１个，求其中至少有两面涂有颜色的概率；
（Ⅱ）从中任取２个小正方体，求２个小正方体涂上颜色的面数之和为４的概率。
（本小题满分10分）
已知向量
，
，函数
（Ⅰ）求
的单调增区间；
（Ⅱ）若
时，的最大值为4，求
的值.