在一个口袋中装有12个大小相同的黑球、白球和红球。已知从袋中任意摸出2个球,至少得到一个黑球的概率是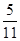 。
。
求:(1)袋中黑球的个数;
(2)从袋中任意摸出3个球,至少得到2个黑球的概率。
如图,四棱锥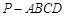 的底面是直角梯形,
的底面是直角梯形,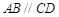 ,
,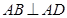 ,
,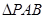 和
和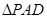 是两个边长为
是两个边长为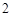 的正三角形,
的正三角形,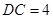 ,
,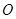 为
为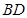 的中点,
的中点,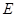 为
为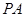 的中点.
的中点.
(Ⅰ)求证: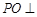 平面
平面 ;
;
(Ⅱ)求证: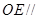 平面
平面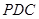 ;
;
(Ⅲ)求直线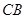 与平面
与平面 所成角的正弦值.
所成角的正弦值.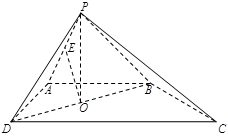
已知椭圆 的焦点分别为
的焦点分别为 、
、 ,长轴长为6,设直线
,长轴长为6,设直线 交椭圆
交椭圆 于A、B两点。(Ⅰ)求线段AB的中点坐标;(Ⅱ)求
于A、B两点。(Ⅰ)求线段AB的中点坐标;(Ⅱ)求 的面积。
的面积。
已知动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半,
求:(Ⅰ)动点M的轨迹方程;
(Ⅱ)若N为线段AM的中点,试求点N的轨迹.
设集合A= ,关于x的不等式
,关于x的不等式 的解集为B(其中a<0),设
的解集为B(其中a<0),设 ,
,  ,且
,且 是
是 的必要不充分条件,求实数a的取值范围.
的必要不充分条件,求实数a的取值范围.
已知函数


 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若函数 的图像在点
的图像在点 处的切线的斜率为
处的切线的斜率为 ,问:
,问:  在什么范围取值时,对于任意的
在什么范围取值时,对于任意的 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值?
(Ⅲ)当 时,设函数
时,设函数 ,若在区间
,若在区间 上至少存在一个
上至少存在一个 ,使得
,使得 成立,试求实数
成立,试求实数 的取值范围.
的取值范围.